How do you find the volume of a rotated region bounded by #y=sqrt(x)#, #y=3#, the y-axis about the y-axis?
2 Answers
Mar 13, 2015
Circular cross sections of the bounded region have an area
or, since
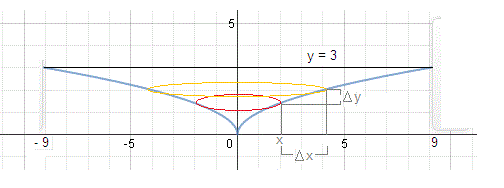
For a thin enough slice,
and the volume of the bounded region would be
Mar 13, 2015
Try this:


