Question

How do you find the volume of solid formed by rotating the region bounded by the graphs: `y=sqrt(x)+5`; y=5; x=1; and x=0; around y=2?

Answer 1

Please see below.

Explanation:

The region described is shown below in blue. A representative slice is taken by the black line inside the region.The axis of rotation is the line `y=2`, shown as a red dashed line. The shorter radius is the black dashed line from `y=2` to `y=5` and the longer radius is the dotted green line from `y=2` to the curve `y = sqrtx+5`

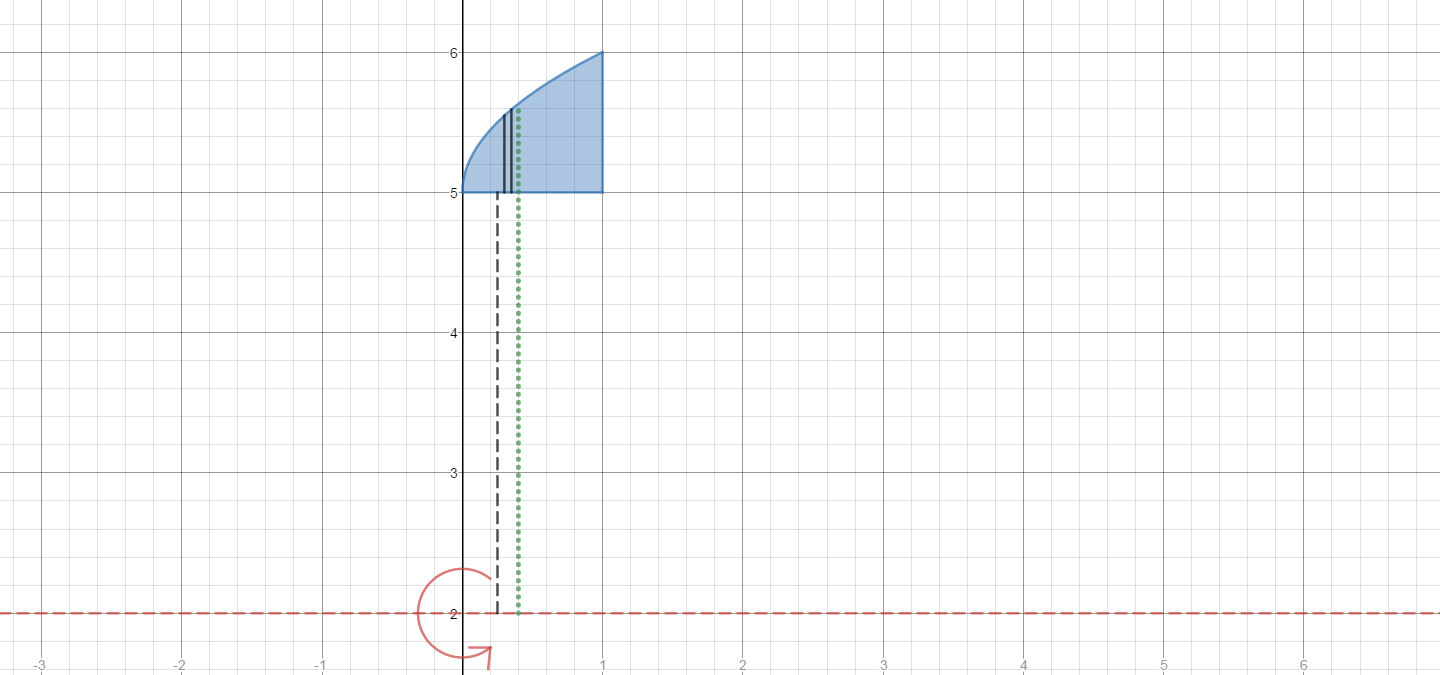
When the slice is rotated the result will be a thin disc (washer).

Let us denote the greater radius by `R` and the lesser by `r`.

The volume of the disc (washer) will be `(piR^2-pir^2) * "thickness"`.

In this picture the thickness is `dx`

`R = (sqrtx+5)-2) = sqrtx+3`

`r = 5 - 2 = 3`

So the representative disc has volume

`pi((sqrtx+3)^2-3^2)dx = pi(x+6sqrtx)dx`

As the final step in setting up the integral, we note that `x` (the variable in the differential `dx`) takes values from `0` to `1`

So the volume of the solid is

`V = int_0^1 pi(x+6sqrtx)dx = (9pi)/2`