How do you find the volume of the region below y= -3x+6 and enclosed by the y-axis from 0 to 2, rotated about the x-axis?
1 Answer
Explanation:
First of all, we have to understand how the region of the plane is made:
The region is determined by this system:
And the points interested are:
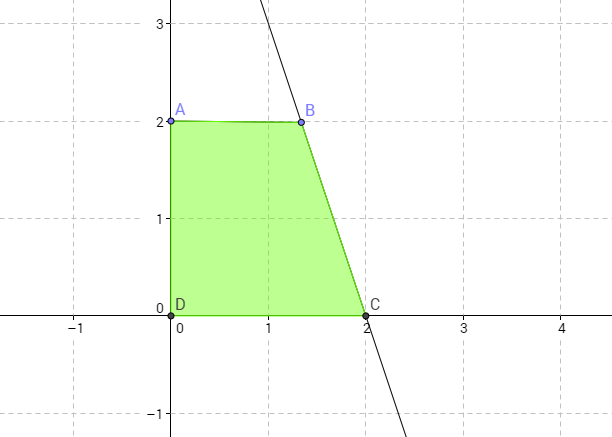 Geogebra
Geogebra
This is the formula for calculating the volume of a solid obtained from a revolution around the x-axis:
But in this case f(x) is a composite function:
So we should break the solid into two rotation solids:
a cylinder from x=0 to x=4/3 and a cone from x=4/3 to x=2: