How do you find the volume of the region bounded by #y=7-x^2#, #x=-2#, #x=2# and the x-axis that is rotated about the x-axis?
1 Answer
Mar 10, 2015
You can see that your solid looks like a football ball with cut ends (even if my graph is a bit crappy!):
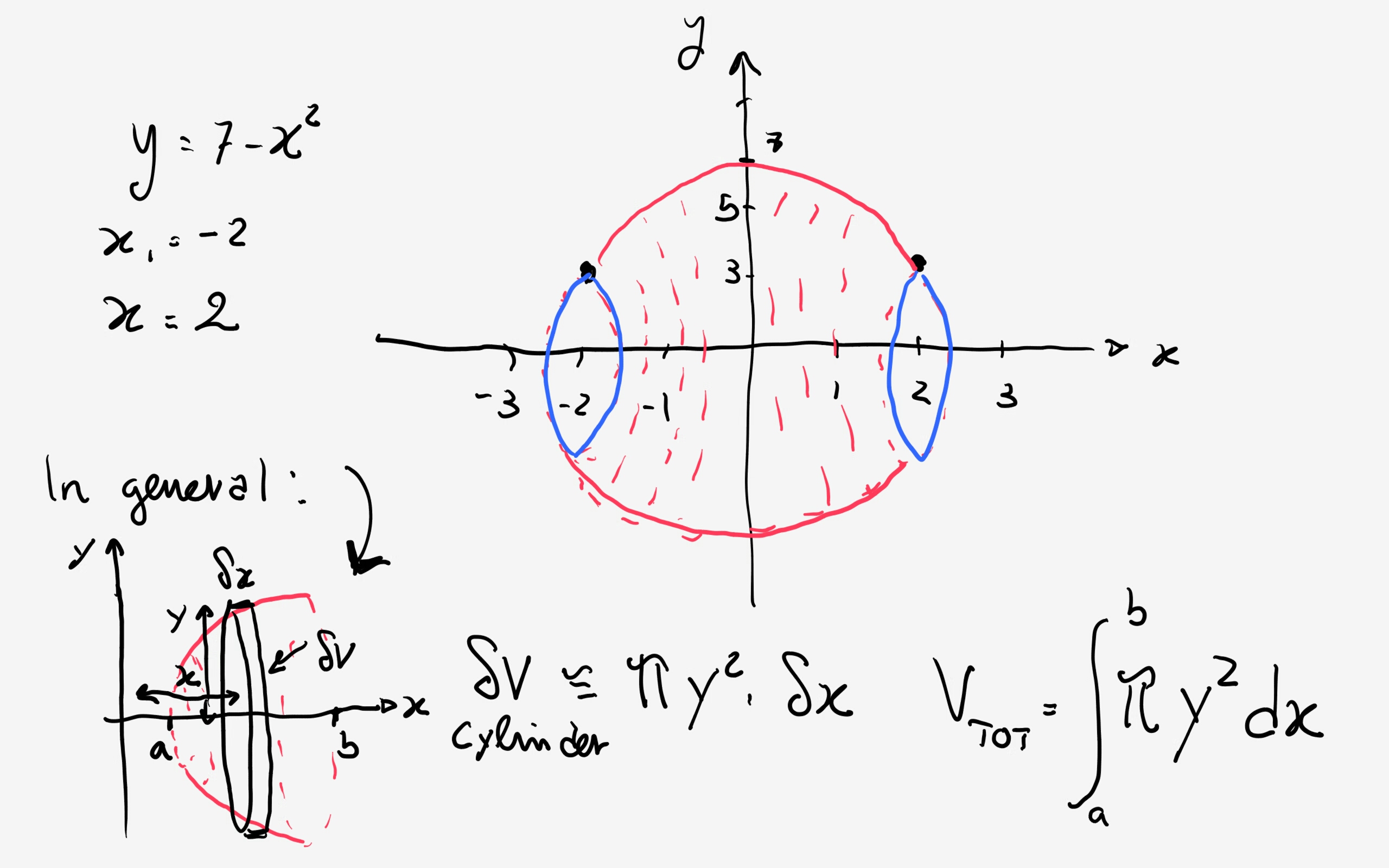
The volume is then:

