How do you find the volume of the region bounded #y = x²# and #y =1# is revolved about the line# y = -2#?

Question

9446 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-10-07T18:11:32

See the explanation.

Here is the region (in blue) with the line #y=-2# in red.

A representative slice in black and the two radii (vertical red lines).

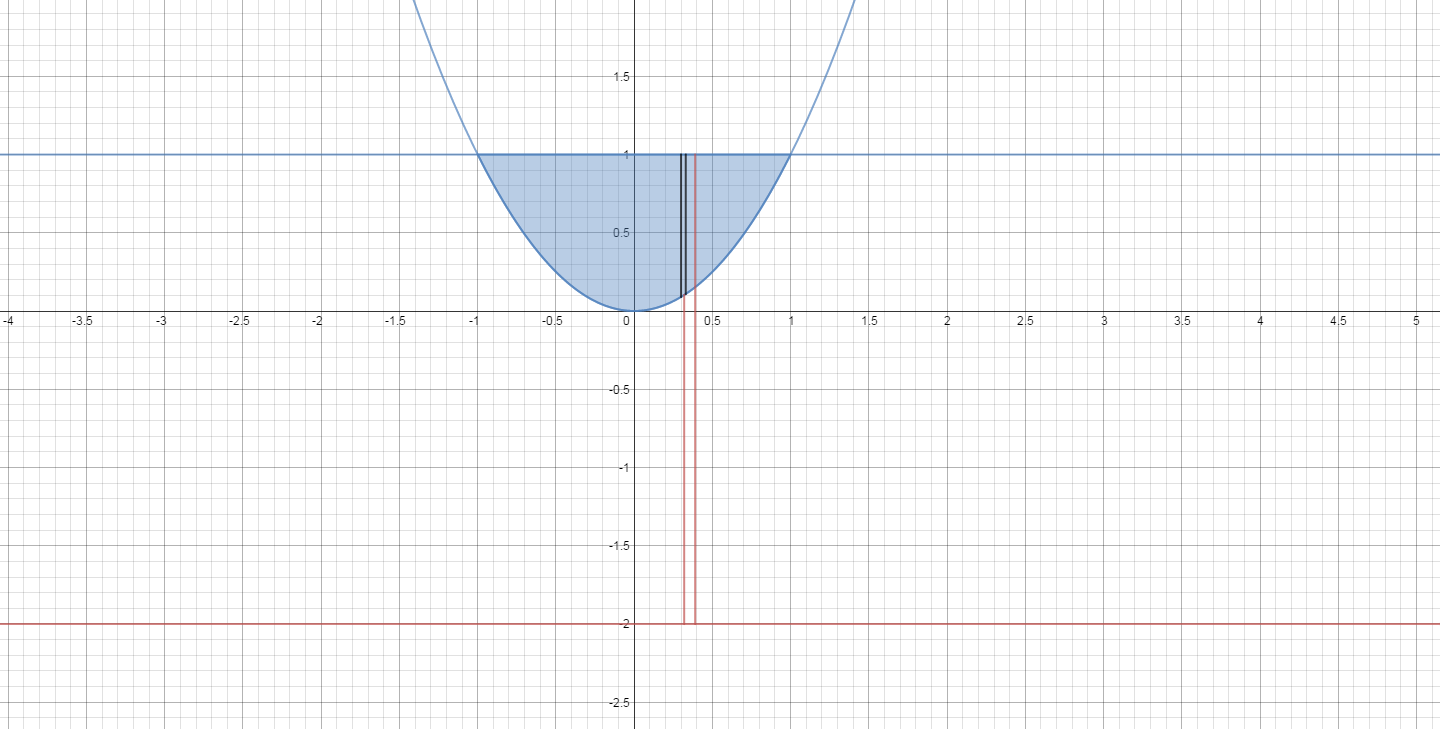
enter image source here

The volume of a washer is #(piR^2-pir^2)dx#
Where #R# is the greater and #r# the lesser radius.

In this question, #R=1-(-2) = 3# and #r=x^2-(-2) = x^2+2#

#x# goes from #-1# to #1#, so we need

#int_-1^1 pi(R^2-r^2)dx = pi int_-1^1(3^2-(x^2+2)^2)dx#

Expand the polynomial integrand and evaluate to get: #104/15pi#