How do you find the volume of the region enclosed by the curves y=2x, y=x^2 rotated about the x-axis?
1 Answer
The volume of the solid generated by
Explanation:
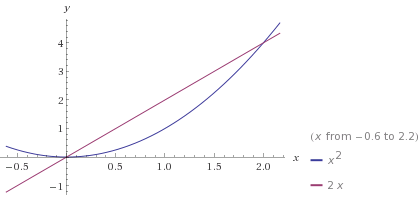 Graph of the two curves
Graph of the two curves
Revolving the area between these two curves about the x-axis, we end up with something that looks sort of like a cone... a hollow cone, with a curved inside. Now, imagine for a second taking a cross section parallel to the y-z plane, cutting the cone down the middle. The cross-section is going to look like a washer, with an inner radius equal to the height of
For reference, the area of a washer is equal to
Now, to find the volume of the solid, we need to sum (integrate) the area of each of cross-sectional washer in the solid. This procedure is commonly called the method of washers .
So, we'll use the method of washers to find the volume of this solid.
The general formula is
where
In our case,
Next, we need to worry about the limits of the integrals. Since we're only concerned with rotating the region between
The difficult part - setting up the appropriate integral with correct limits - is done, so I won't walk through evaluating the integral. It evaluates to

