How do you find the volume of the solid formed by revolving a particular region around the x-axis given #y=2#, #y=4-(x^2/2)# and bounded from [-2,2]?
1 Answer
Apr 10, 2015
This is a very good question indeed!!!!
First have a look at the region on the
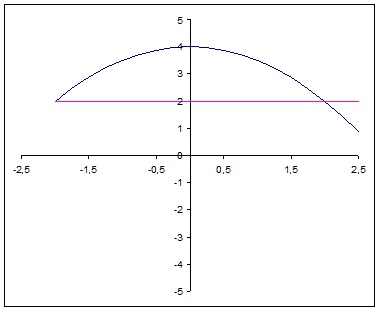
Basically when this region rotates about the
To evaluate the volume you can first rotate the curved part alone and get its volume (a barrel) and then subtract the volume obtained rotating the straight line alone (a cylinder) as in:
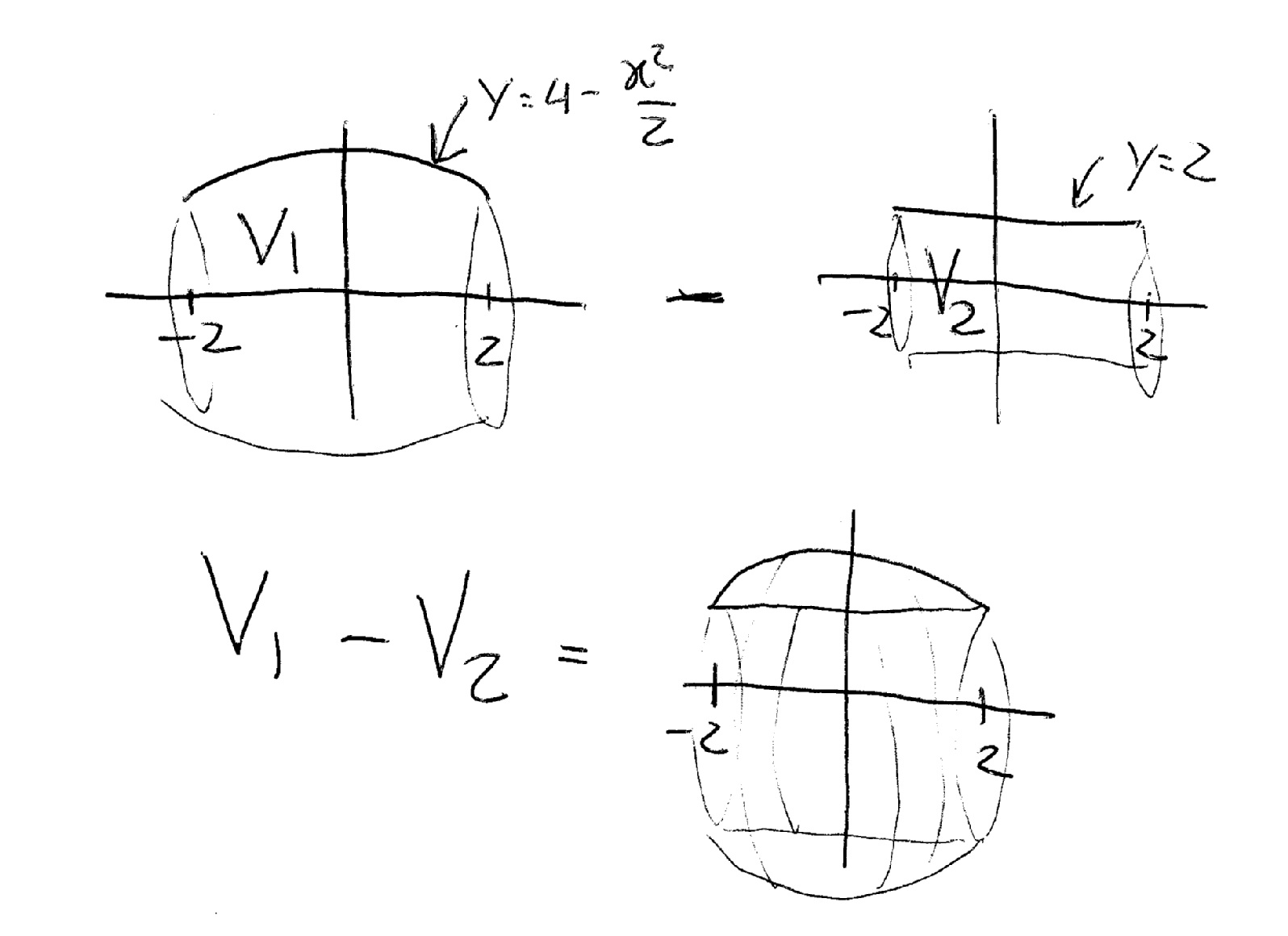
To evaluate each volume I use a small cylinder of radius
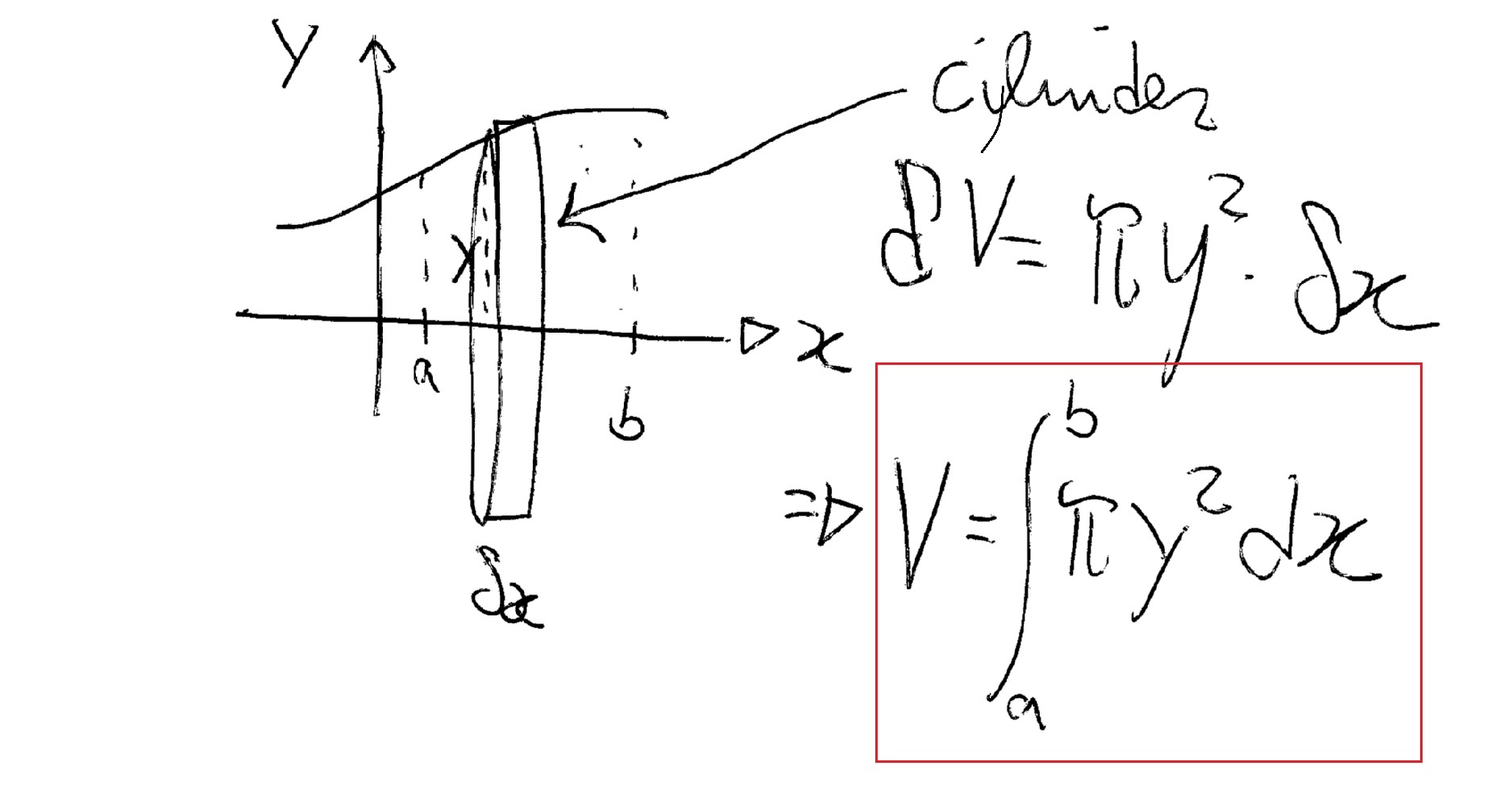
So that:
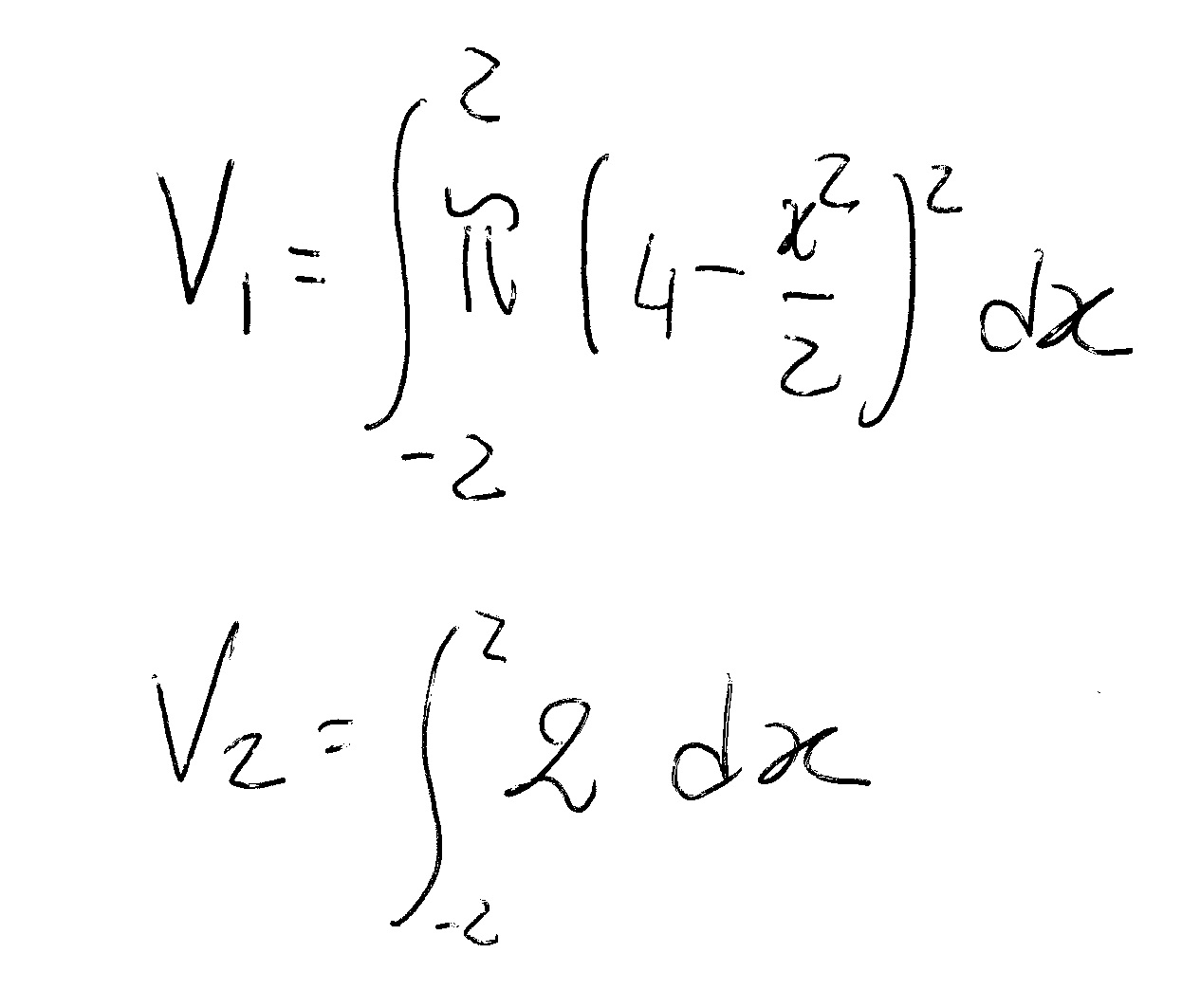
And finally:
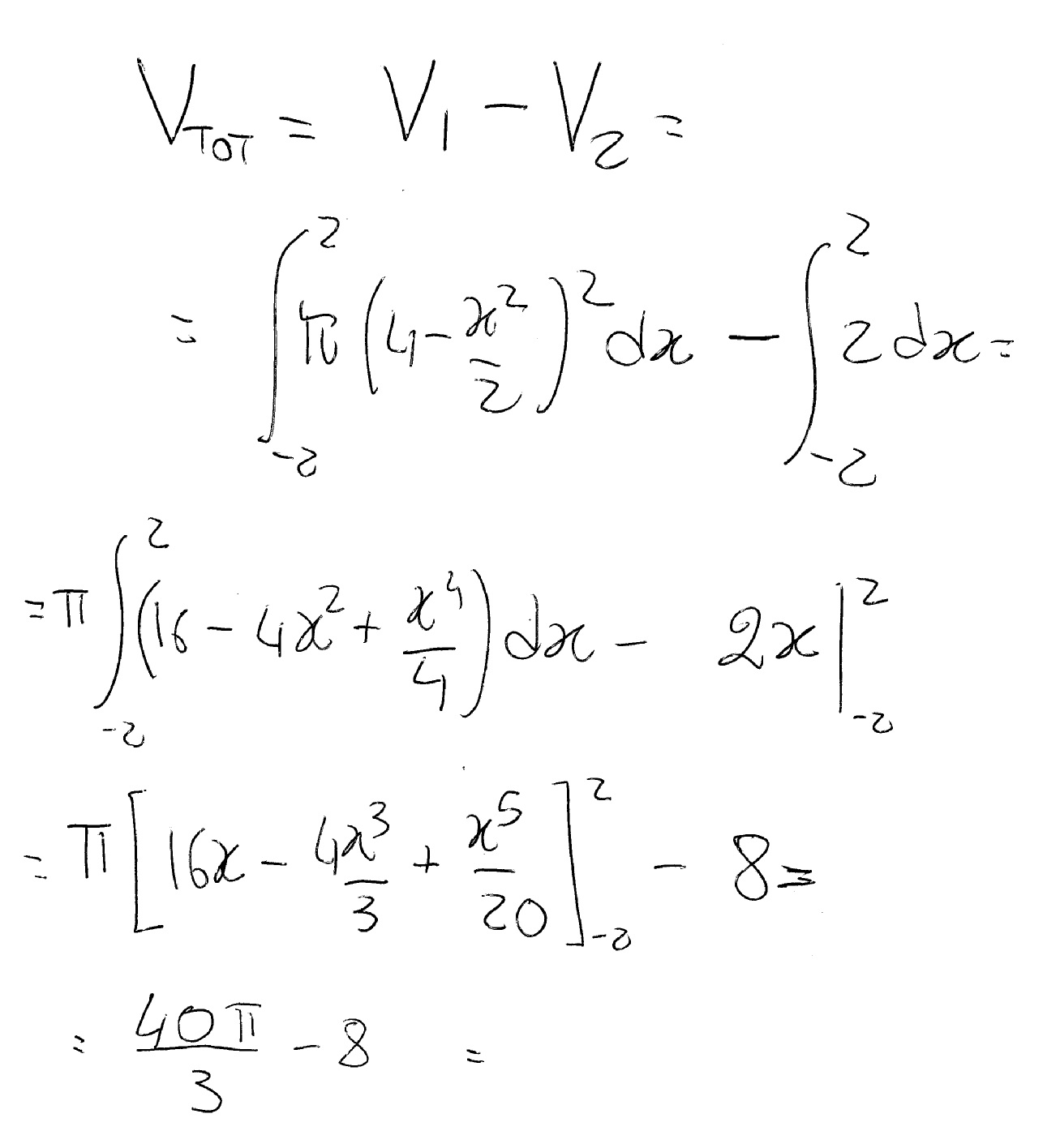
Hope it helps but PLEASE check my maths!

