Question

How do you find the volume of the solid generated by revolving the region bounded by the curves y = x² and y =1 rotated about the y=-2?

Answer 1

See the explanation below.

Explanation:

Here is a picture of the region and a vertical slice.

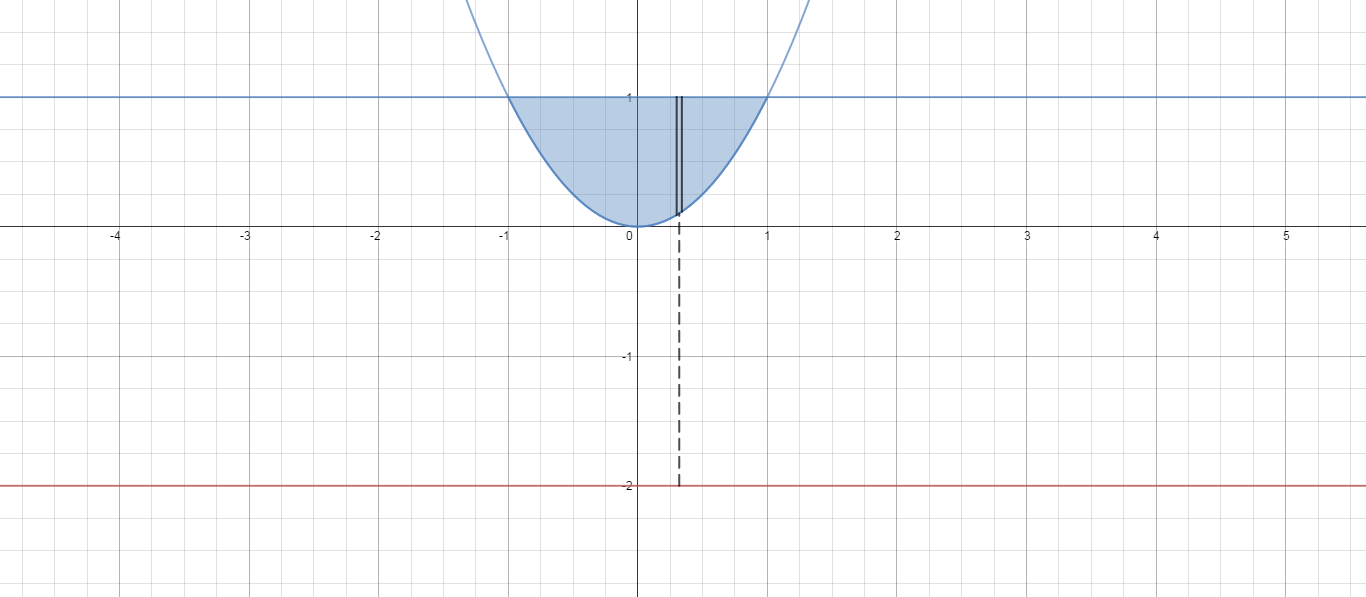
The picture is set up to use washers (disks).
Thickness is `dx`
`x` values go from `-1` to `1`
the radius of the larger washer is the greater `y` minus `-2` (the line we are revolving about is `y=-2`)
`R = 1-(-2) = 3`
the radius of the smaller washer is the lesser `y` minus `-2`
`r=x^2-(-2) = x^2+2`

The representative slice has volume `pi(R^2-r^2)dx`.

We need to evaluate the integral

`int_-1^1 pi((3^2-(x^2+2)^2)dx=pi int_-1^1(5-4x^2-x^4)dx`

`= 104/15pi`

Shells Method
If we had taken a slice horizontally:

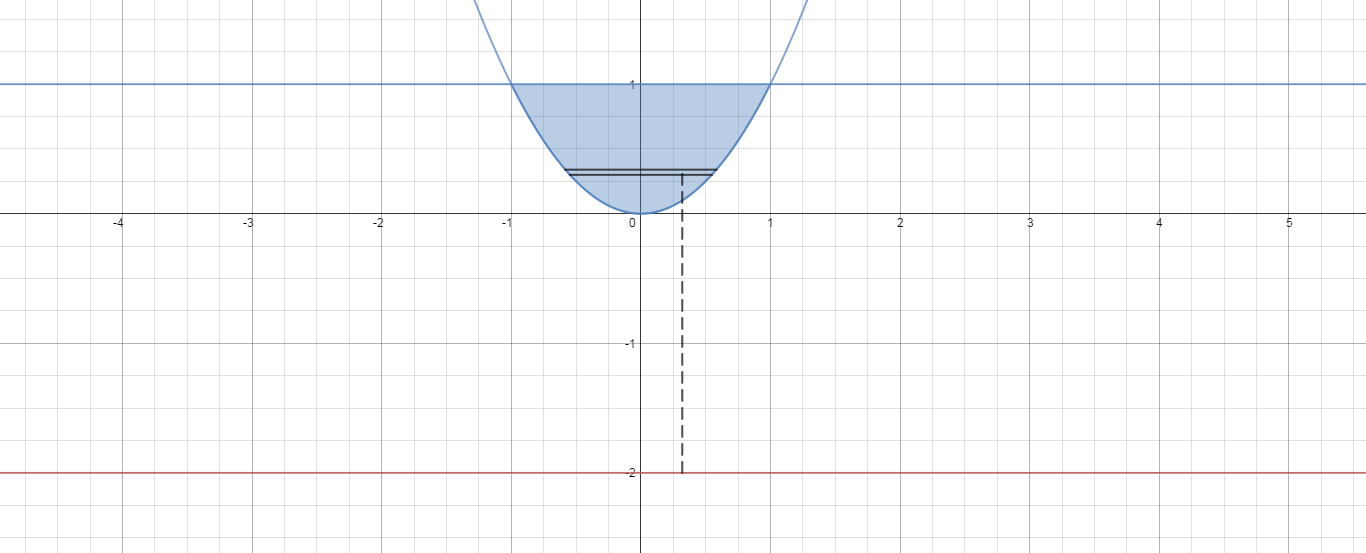
This is set up to use cylindrical shells of thickness `dy`

The volume of each shell is `2pi("radius")("height")("thickness")` with thickness `dy`, that is `2pi*rh*dy`
In the region, the `y` values go from `0` to `1`.
The radius of the representative shell is `y+2` (dotted line in picture)
The height goes from the greater `x` (the one on the right) to the lesser `x` (the one on the left).
We need to rewrite the boundary as functions of `y` instead of `x`. `y=x^2` becomes the two functions `x=-sqrty` (on the left) and `x=sqrty` (on the right). The height of the shell is `sqrty-(-sqrty) = 2sqrty`

The representative shell has volume `2pi(y+2)(2sqrty)dy`.

The solid has volume

`V = int_0^1 2pi(y+2)(2sqrty)dy = 4piint_0^1 (y^(3/2)+2y^(1/2))dy`

`=4pi(26/15) = 104/15 pi`