How do you find the volume of the solid generated by revolving the region bounded by the curves y = x^(1/2), y = 2, and x = 0 rotated about the x=-1?
1 Answer
Explanation:
Refer to the figure below
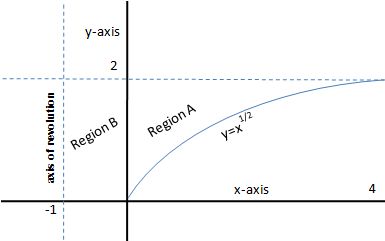 I created this figure using MS Excel
I created this figure using MS Excel
The generator region is Region A limited by
Since the revolution is around an axis parallel to the y-axis, it's convenient to use the inverse function
We can use a trick to solve this problem: translating the y-axis to the position of the axis of the revolution. Consequently
We only have to remember to exclude Region B, since now the old
Applying the formula for volume of a solid of revolution (with a hole), with axis of revolution in y-axis:
V=pi int_a^b [R(y)^2-r(y)^2]*dy , whereR(y) is the external radius andr(y) is the internal radius
V=pi int_0^2 [(y^2+1)^2-1^2]*dy
V=pi int_0^2 (y^4+2y^2+cancel1-cancel1)*dy
V=pi int_0^2 (y^4+2y^2)*dy
V=pi (y^5/5+2/3y^2)|_0^2
V=pi(32/5+2/3*8)=pi(96+80)/15=(176pi)/15~=36.86 [cubic units]

