How do you find the volume of the solid generated by revolving the region bounded by the graphs #x=y^2, x=4#, about the line x=6?
1 Answer
Mar 31, 2017
Please see below.
Explanation:
The graph of the region is shown below. A representative slice of thickness
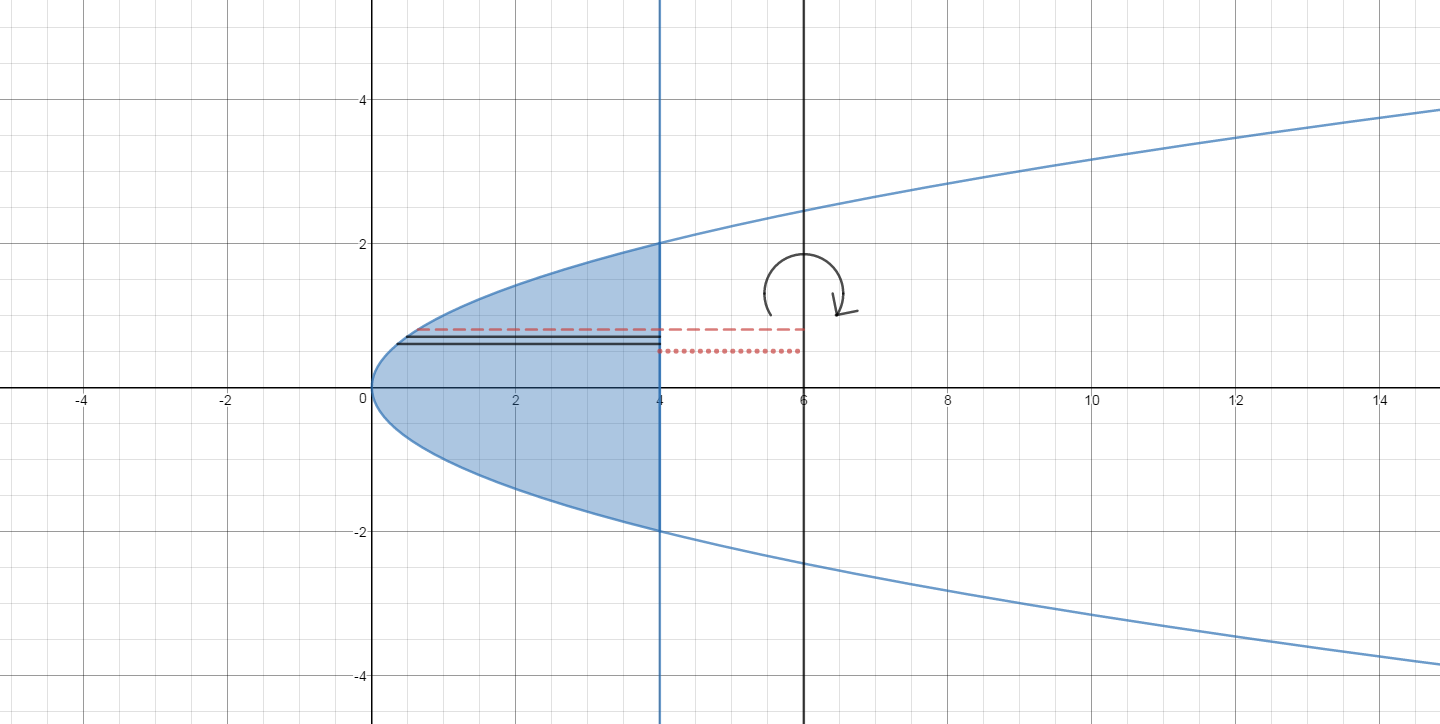
When revolved about the line
In this problem
#R = 6-y^2# and
#r = 6-4=2# and
#"thickness" = dy# .
So the volume of the solid of revolution is
# = (384pi)/5#
or about

