How do you find the volume of the solid generated by revolving the region bounded by the graphs #xy=6, y=2, y=6, x=6#, about the line x=6?
1 Answer
Please see below.
Explanation:
Find the volume of the solid generated by revolving the region bounded by
Here is a graph. The region is in blue. A representative slice (black line segments) has been taken at a
The axis of revolution is the line
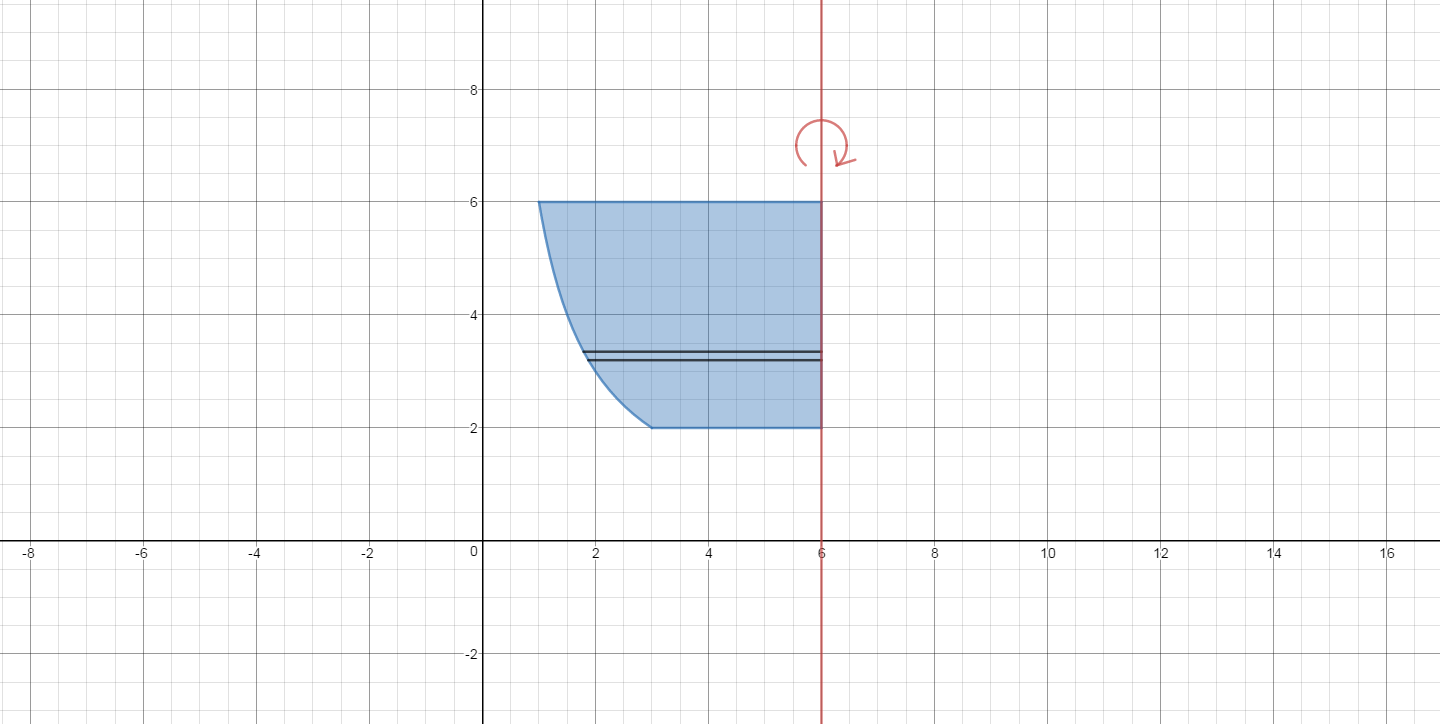
Because the thickness is the differential of
When rotated, the radius is the
The volume of the representative disk is
# = pi(36-72/y+36/y^2)dy#
# = pi(156 - 72ln(3))#

