How do you find the volume of the solid generated by revolving the region bounded by the graphs #y=e^(x/2), y=0, x=0, x=4#, about the x axis?
1 Answer
Dec 15, 2016
Please see below.
Explanation:
Here is a graph of the region in blue. A slice has been taken perpendicular to the axis of rotation. The rotation as shown by the arrow/arc.
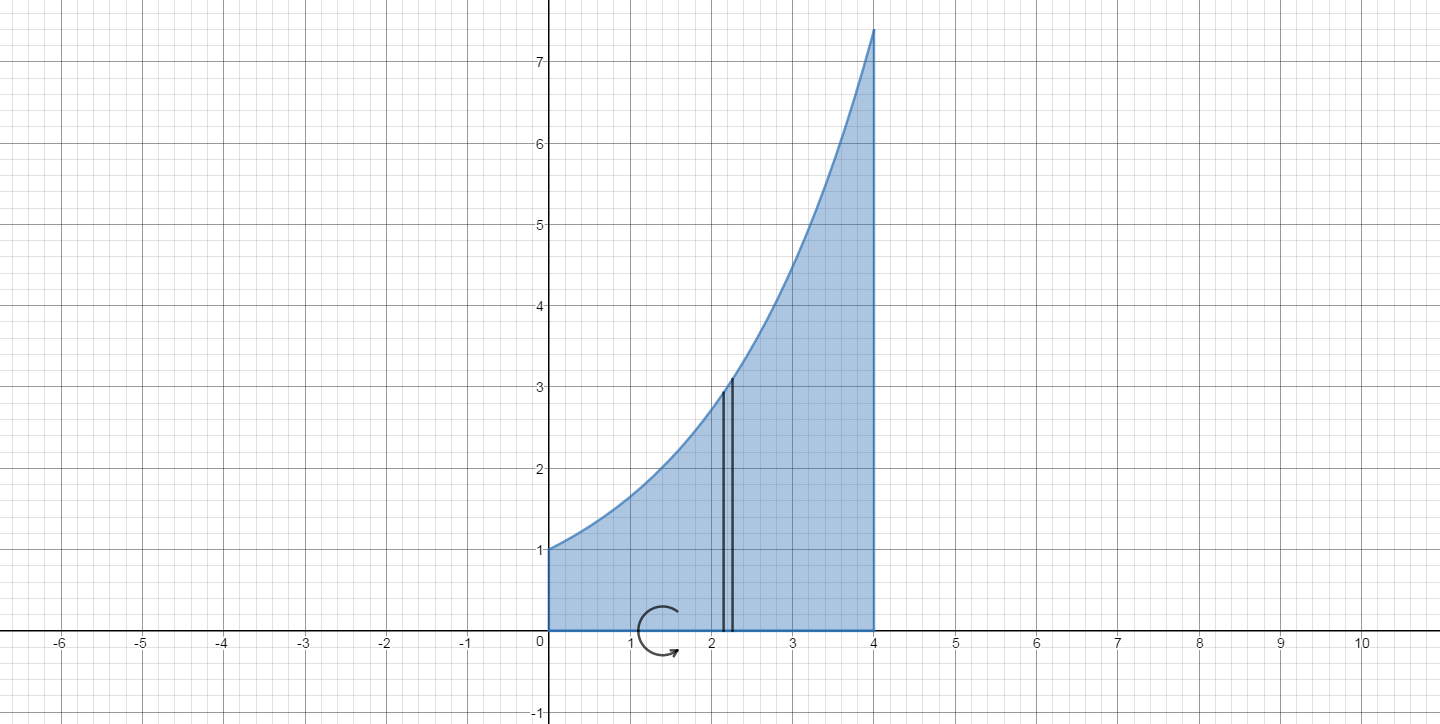
The representative slice is a disc of
thickness dx
and radius
The volume of the representative slice (disc) is
The values of
Evaluate the integral to get

