Question

How do you find the volume of the solid generated by revolving the region bounded by the graphs `y=3(2-x), y=0, x=0`, about the y axis?

Answer 1

Volume `= 8pi`

Explanation:

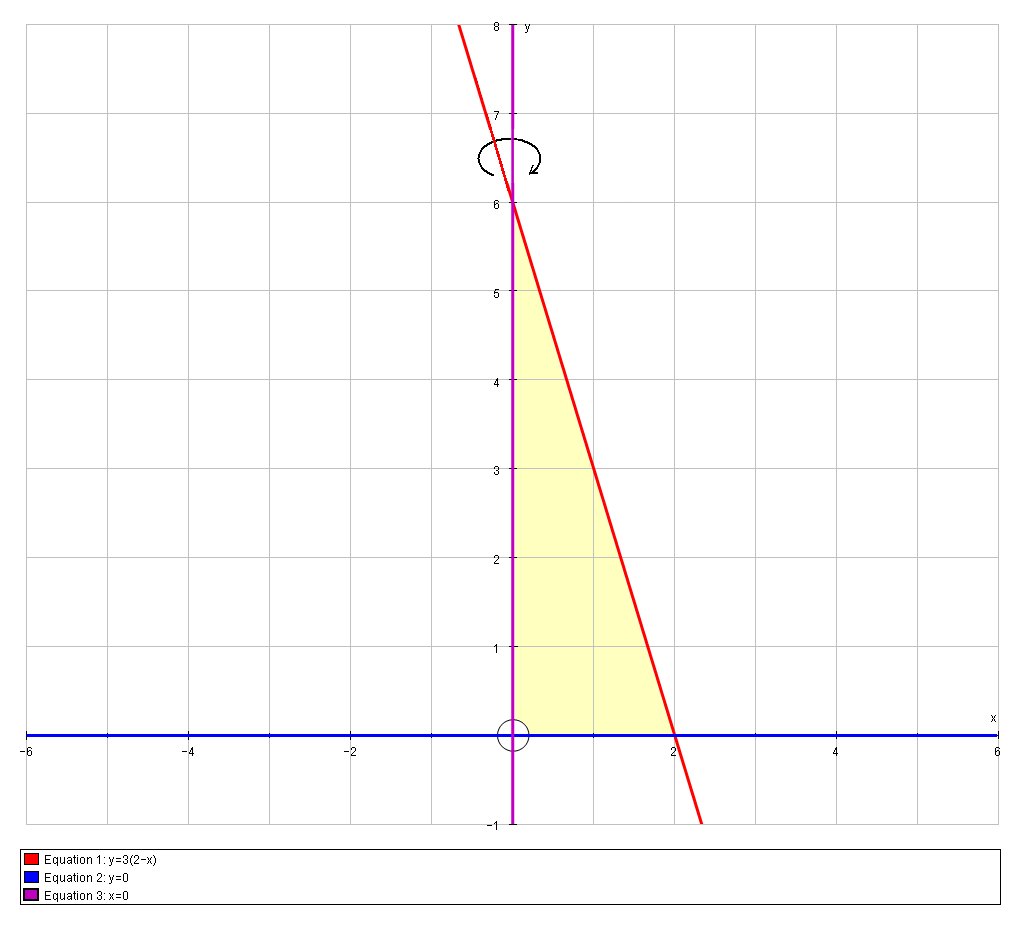
When `y(2-x)` is rotated about the `y`-axis it will generate a cone of base radius `2` and height `6`, hence the volume is:

`\ \ \ \ \ V =1/3pir^2h`
`:. V = 1/3pi*2^2*6`
`:. V = 8pi`

If you want a calculus solution, then the Volume of revolution about the `y`-axis is given by:

`V =int_a^b pi x^2dy`

Now:

`y=3(2-x) => y=6-3x`
`:. x=1/3(6-y)`

And so:

`V = int_0^6 pi (1/3(6-y))^2 \ dy`
`\ \ \ = 1/9 pi int_0^6 (6-y)^2 \ dy`
`\ \ \ = 1/9 pi int_0^6 (36-12y+y^2) \ dy`
`\ \ \ = 1/9 pi [36y-6y^2+1/3y^3]_0^6`
`\ \ \ = 1/9 pi {(36*6-6*36+216/3) - (0)}`
`\ \ \ = 1/9 pi (72)`
`\ \ \ = 8 pi`