This problem involves finding the volume of a solid of revolution about a disk. Don't let the #y^2# part of this problem scare you. It actually makes the solving the problem a bit easier. Remember that solving for #y# in the above equation would involve a #+-sqrt()#, (i.e., a positive and negative square root). This results in:
#y_1=+sqrt(x(4-x)^2)#, and
#y_2=-sqrt(x(4-x)^2)#
However, because the process of finding the volume of a solid of revolution around the x-axis involves squaring your expression, it won't matter if you use the positive or negative version. So we'll use the positive.
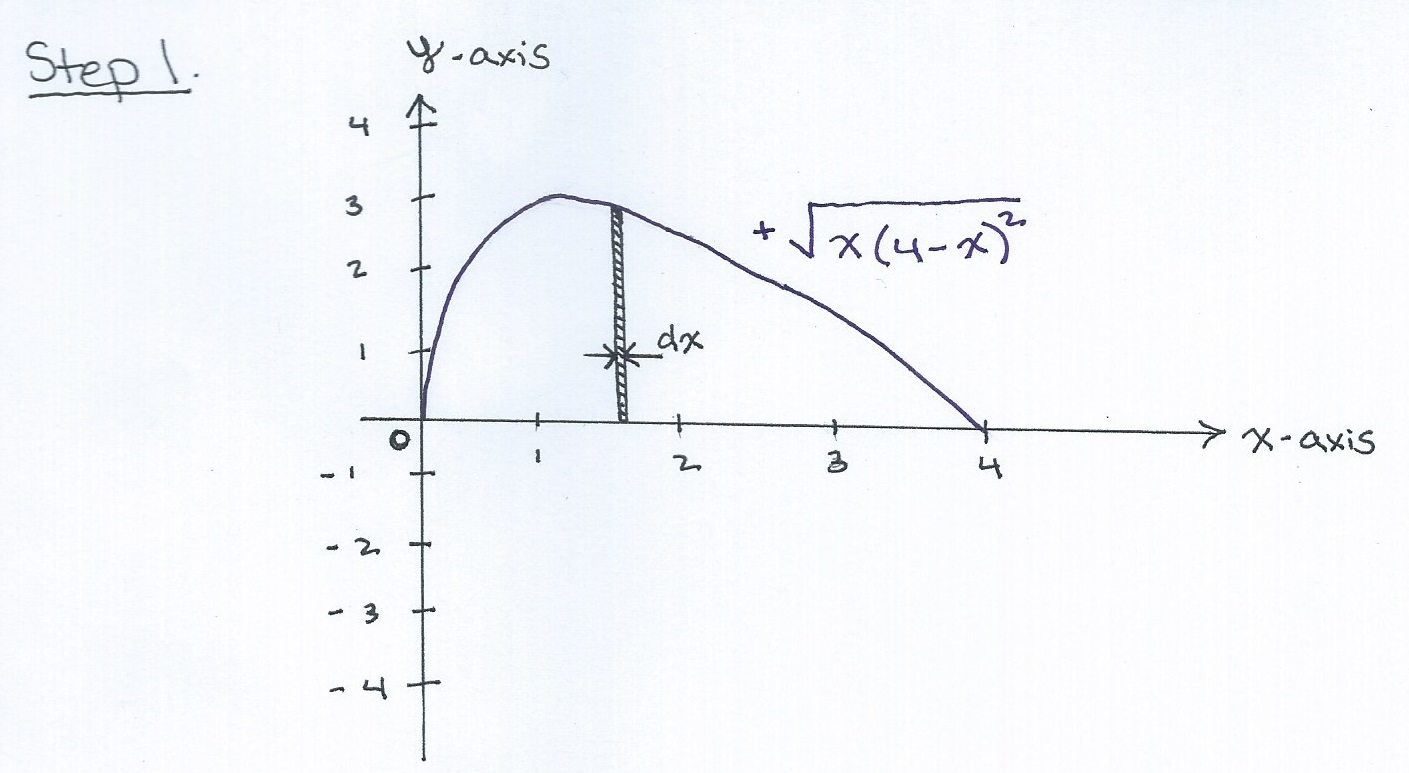
Step 1. Sketch the region that is going to be revolved and label your boundaries. Also, because the expression in #y_1# is in terms of #x#, we will also need to sketch a thickness rectangle #dx#. This will be the disc we ultimately integrate over.
Step 2. Sketch the 3D solid generated by the region under the curve and the disc formed by the #dx# rectangle (i.e., the thickness). This is where being an artist really pays off in calculus! Below, I tried to show the disc and the teardrop shape of the graph
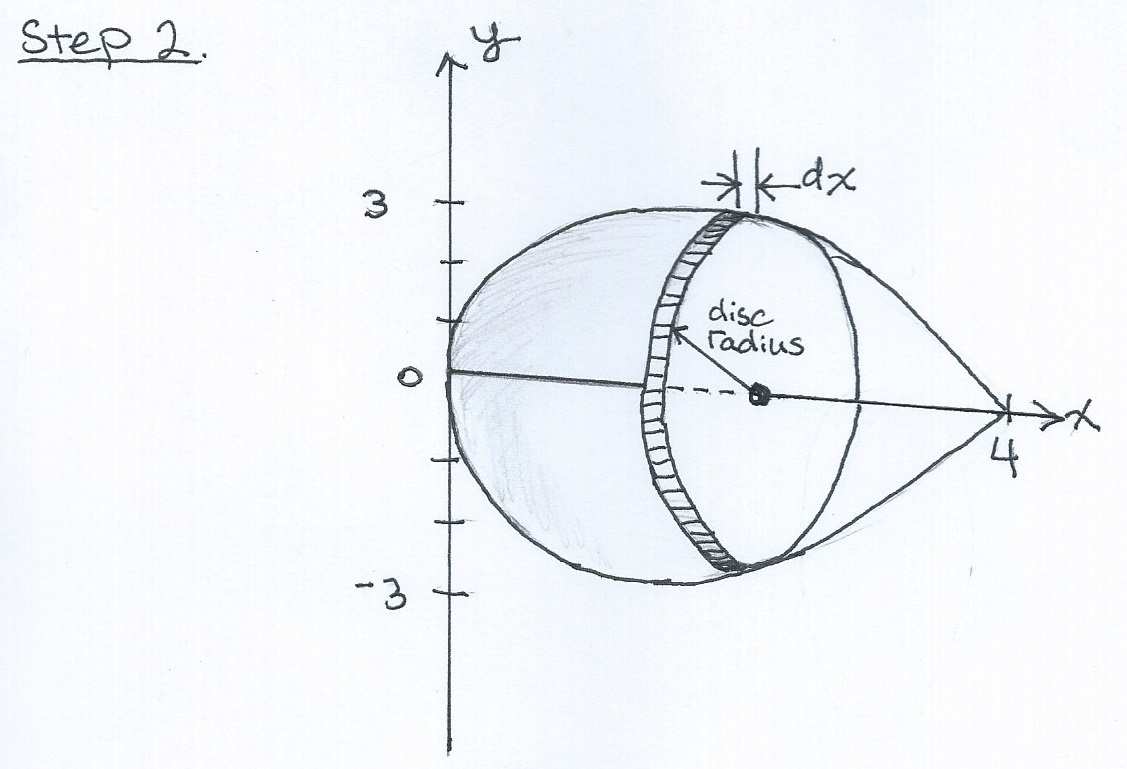
Step 3. It should be clear that the radius is really just the equation #"radius"=y=sqrt(x(4-x)^2)#. The volume of the circular disc is basic geometry. The area of a circle is #A_"circle"=pir^2# (a common mistake is to say #A_"circle"=2pir^2#, which is confused with the perimeter of a circle, #P = 2pir#). So the volume of a disc is #(A_"circle")*("thickness")=A_"circle"*dx#.
#V_"disc"=A_"circle"*dx#
#V_"disc"=pir^2dx#
#V_"disc"=pi(sqrt(x(4-x)^2))^2dx#
#V_"disc"=pix(4-x)^2dx#.The square and square root cancel.
Step 4. Find the volume of the solid by integrating over #x=0# to #x=4#.
#V_"solid" = int_0^4(V_"disc")#
#V_"solid" = int_0^4pix(4-x)^2dx#
#V_"solid" = pi int_0^4x(4-x)^2dx#
#V_"solid" = pi int_0^4x^3-8x^2+16xdx#
#V_"solid" = pi(x^4/4-8x^3/3+8x^2)|_0^4#
#V_"solid" = pi(4^4/4-8(4^3)/3+8(4^2))#
#V_"solid" = (64pi)/3=21(pi/3)#


