How do you find the volume of the solid obtained by rotating the region bounded by the curves #y=x^2# and #y=2-x^2# and #x=0# about the line #x=1#?
1 Answer
I would use shells (to avoid doing two integrals).
Explanation:
Here is a picture of the region. I have included the axis of rotation (
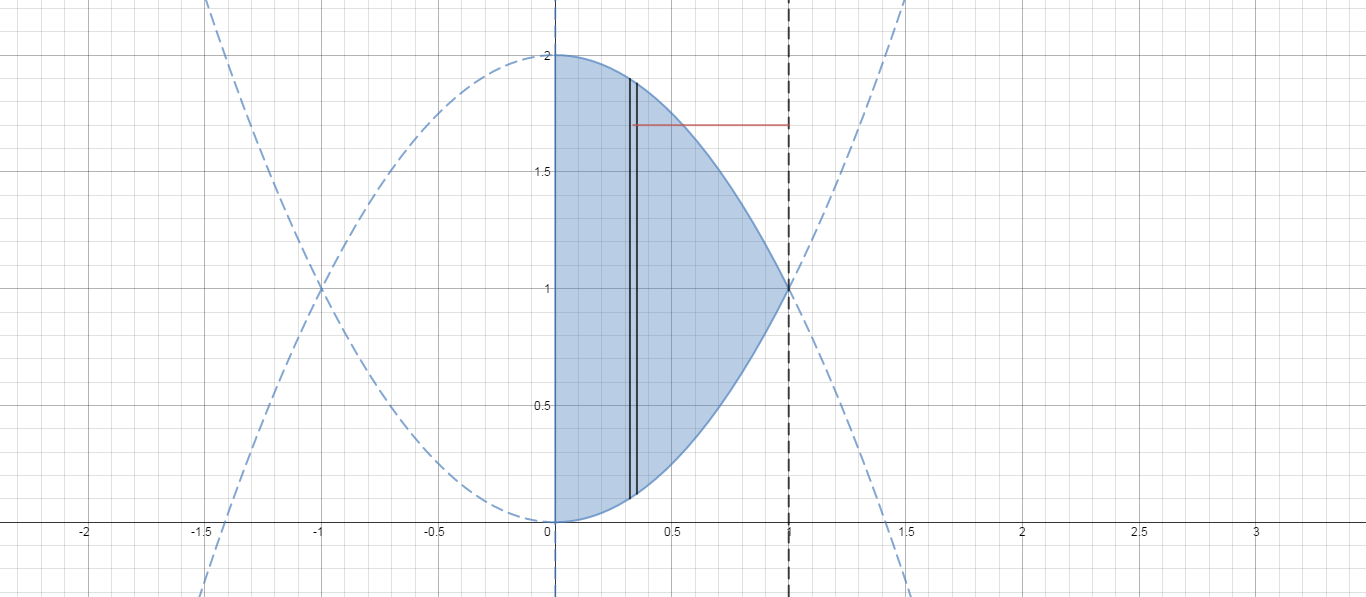
When we rotate the slice, we'll get a cylindrical shell.
The representative cylindrical shell will have volume:
#2 pixx"radius"xx"height"xx"thickness"# .
Here we have:
The height will be the greater
We also not that in the region,
Using shell, the volume of the solid is found by evaluating:
So we need
# = 2piint_0^1 (2-2x-2x^2+2x^3) dx#
# = 5/3 pi#

