How do you find the volume of the solid obtained by rotating the region bounded by the curves #x=y-y^2# and the y axis rotated around the y-axis?
1 Answer
Jul 29, 2015
Explanation:
The curve represents a horizontal parabola as seen in the picture
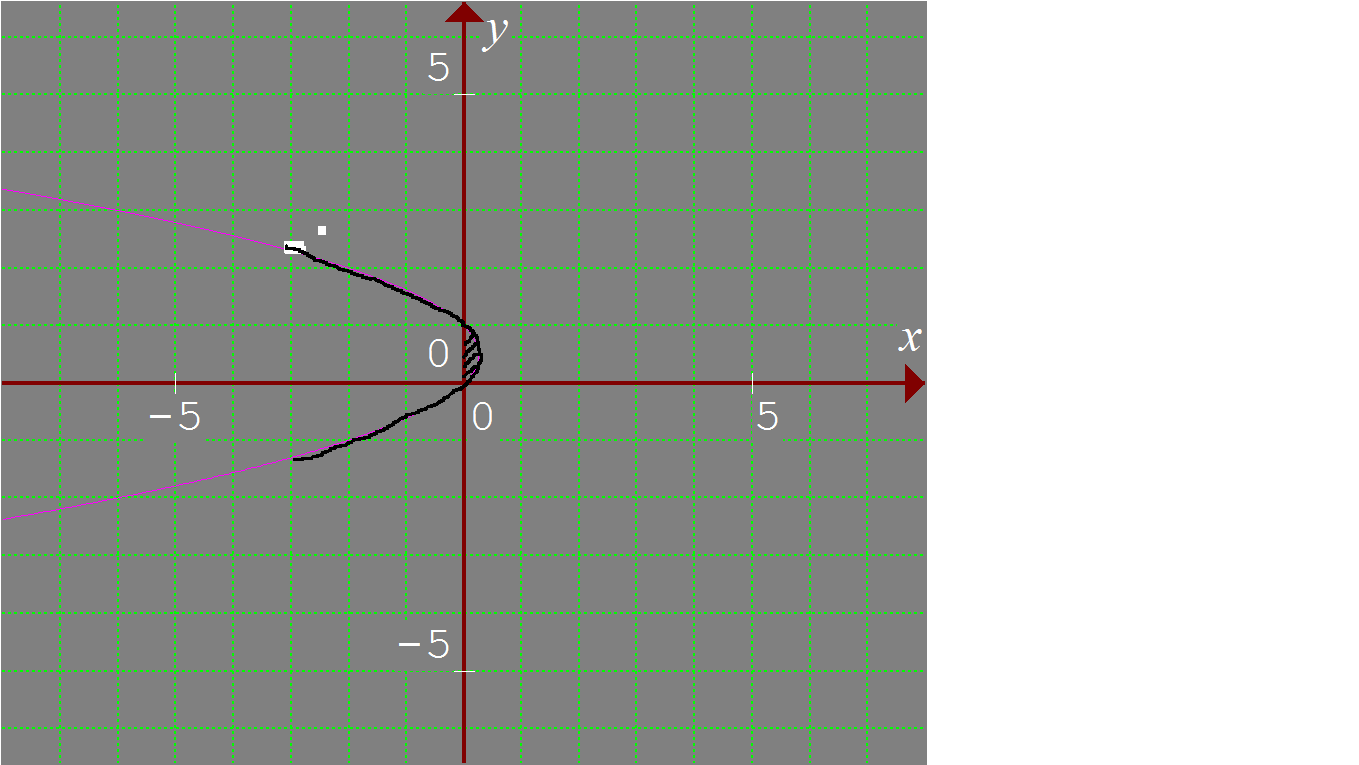
The region rotated about y axis is the shaded region.
The volume of the solid so generated would be(consider an elementary strip of length and thickness
=
=
=
=
