How do you find the volume of the solid obtained by rotating the region bounded by the curves #y=sqrtx# and #y=x/3# rotated around the #x=-1#?
1 Answer
See the explanation section, below.
Explanation:
Here is a picture of the region (in blue) and the line
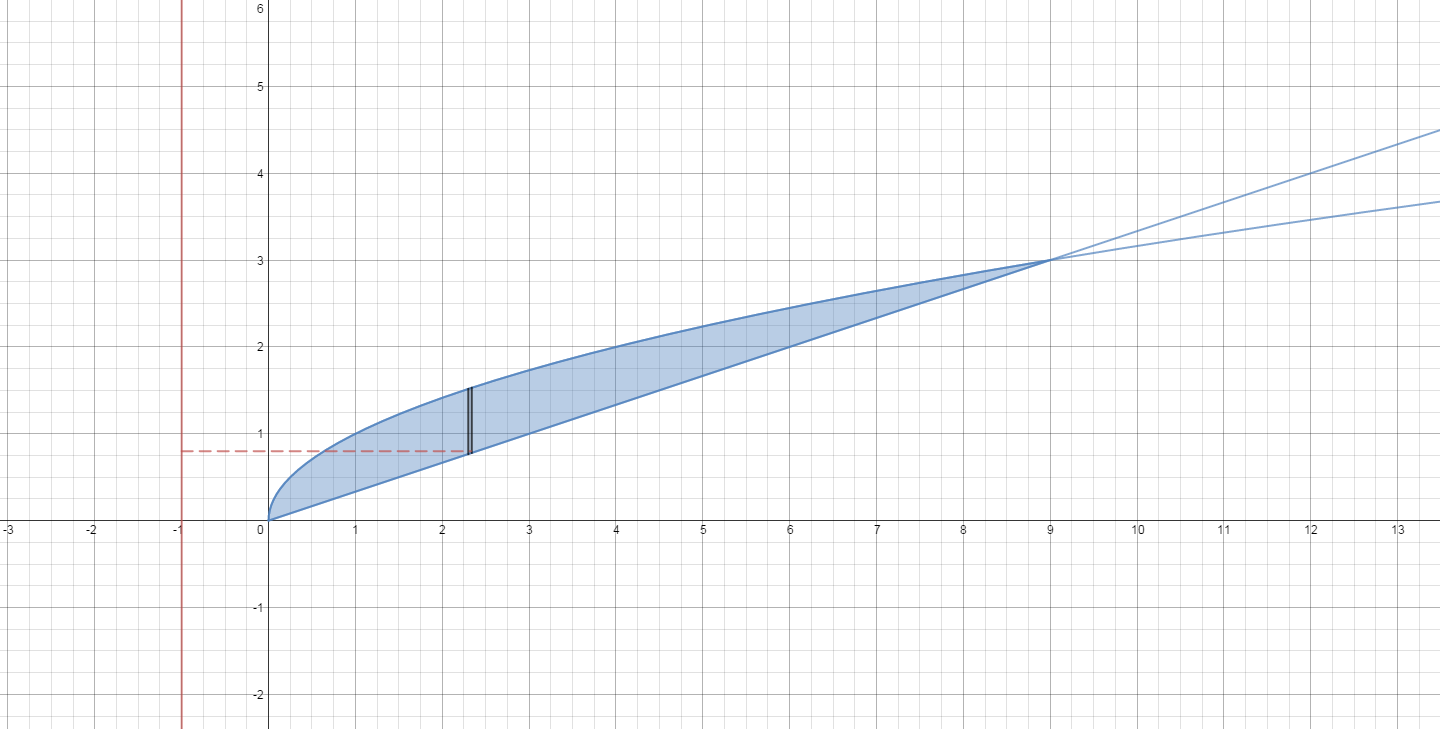
It shows a representative slice of thickness
The volume of the shell is
The height of the shell is the greater
We also need the point of intersection where
The integral we need to evaluate is:
Expand the integrand to get 4 terms in powers of

