Given: #1/(1+x^2)#, bound in the region, #R# over #y=0, x=0, and x=2# rotated around #x=2#
Required Volume?
Solution Strategy: Use the "Volume by Cylindrical Shells Method"
The "shell method" give the volume calculated in the region bound by #y = f (x), a ≤ x ≤ b# and the integral formula is:
#V_s=∫_a^b 2π ("shell radius") ("shell height") dx=2pi∫_a^br_sh_sdx#
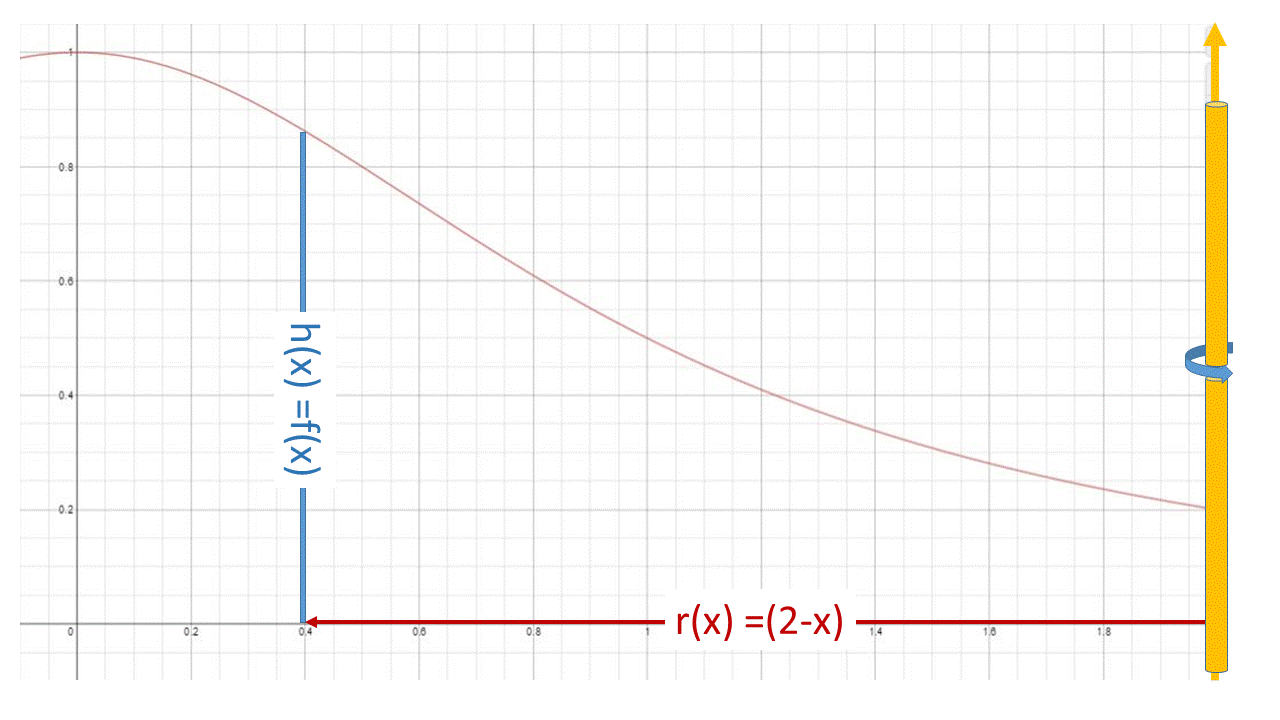
From the figure #r_s(x) = (2-x) and h_s(x) = f(x)=1/(1+x^2)#
thus#=>V_s=2pi∫_a^b r_s(x)*f(x) dx#
#V_s=2pi∫_a^b (2-x)*1/(1+x^2) dx # Now simply integrate
Apply sum rule and write:
#V_s=2pi[∫_a^b 2/(1+x^2)dx - ∫_a^bx/(1+x^2)dx] =2pi[I_1-I2]#
#I_1 =∫_a^b 2/(1+x^2)= [2arctan(x)]_0^2#
#I_2= ∫_a^bx/(1+x^2)dx # let #u=1+x^2; du=2xdx; dx=1/(2x)du #
#I_2= ∫cancelx/u 1/(2cancelx)du=1/2ln(u)# substitute #u=1+x^2#
#I_2=1/2ln(1+x^2)#
#V_s= 2pi[I_1-I_2 ] = 2pi[2arctan(x)+1/2ln(1+x^2)]_0^2= #
#V_s = 2pi[2arctan(2)-1/2ln(5) ]#


