Question

How do you find the volume of the solid obtained by rotating the region bounded by the curves `y = x^3`, `x=0`, and `x=1` rotated around the `y=-2`?

Answer 1

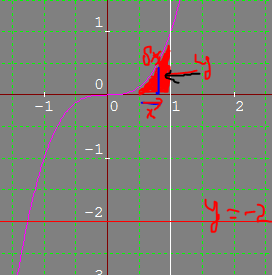
The region to be rotated about y=-2 is shown here shaded in red.
Consider an element of length y and width `delta`x at a distance x from the origin. If this this is rotated about y=-2. It would form a circular disc of radius y+2. Its area would be `pi (y+2)^2`. Its volume would be `pi (y+2)^2 delta x` From this subtract the volume of coaxial region `pi 2^2 delta x`

Required volume is that of the annular region `pi (y+2)^2 delta x -4pi delta x`

=`pi(y^2 +4y)delta x`.

The volume of the solid formed by the whole region would therefore be

`int_(x=0)^1 pi (y^2 +4y) dx`. Since y is =`x^3`

Integral to solve would be `int_(x=0)^1 pi (x^6 +4x^3)dx`

= `pi[x^7 /7 +4 x^4 /4]_0^1`
= `(8pi)/7`