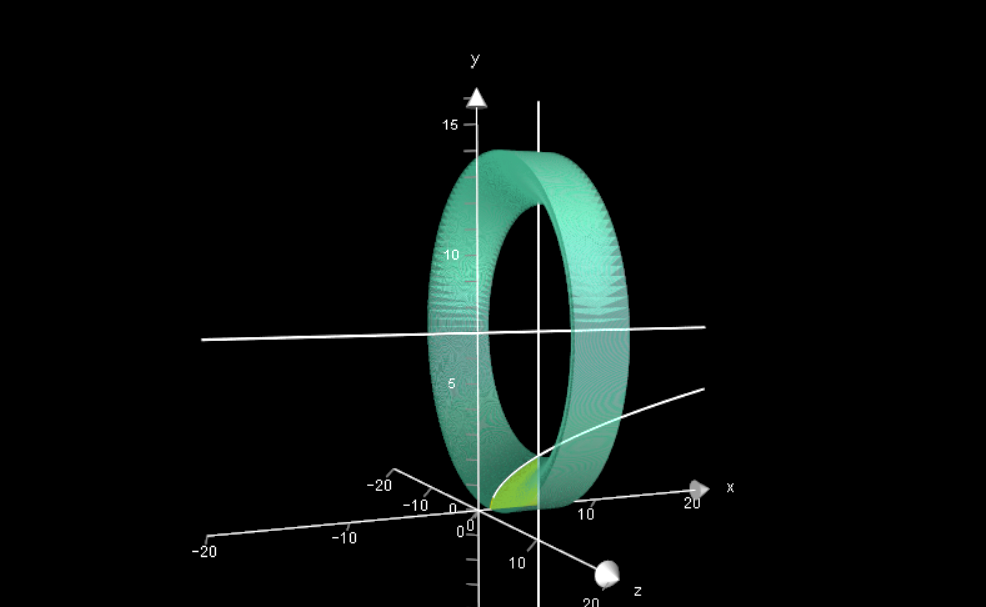
How do you find the volume of the solid obtained by rotating the region bounded by: #y=sqrt(x-1)#, y=0, x=5 rotated about y=7?
2 Answers
Please see below.
Explanation:
I would use shells. Here is a picture of the region with a slice taken parallel to the axis of rotation.
The slice is taken at a value of
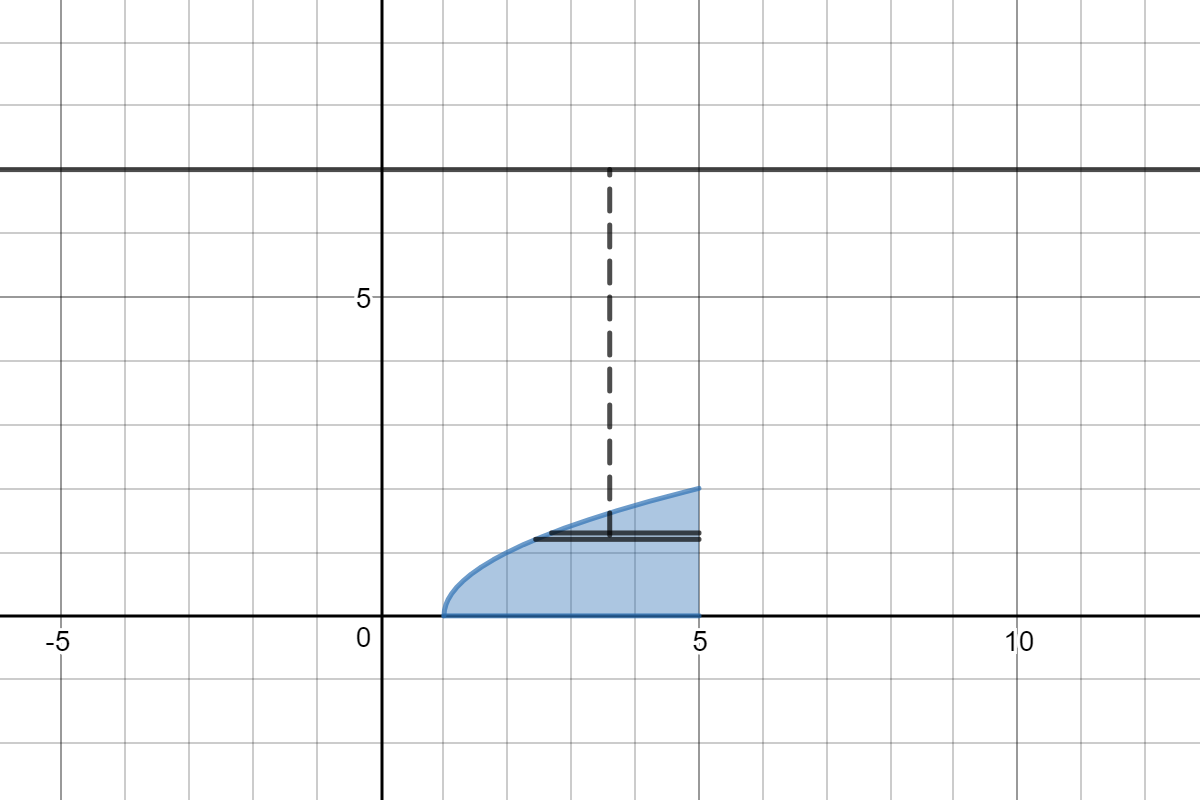
The thickness of the slice and the shell is
The radius is
The height is
The shell has volume
The resulting solid has volume:
# = 2piint_0^2(28-4y-7y^2+y^3) dy#
# = 2pi[28y-2y^2 - 7/3y^3+y^4/4]_0^2#
#= (200pi)/3#
If you prefer washers
Then the thickness is
the greater radius is
the lesser radius is
# = pi int_1^5(14sqrt(x-1) - (x-1))dx#
To integrate I would substitute
See below.
Explanation:
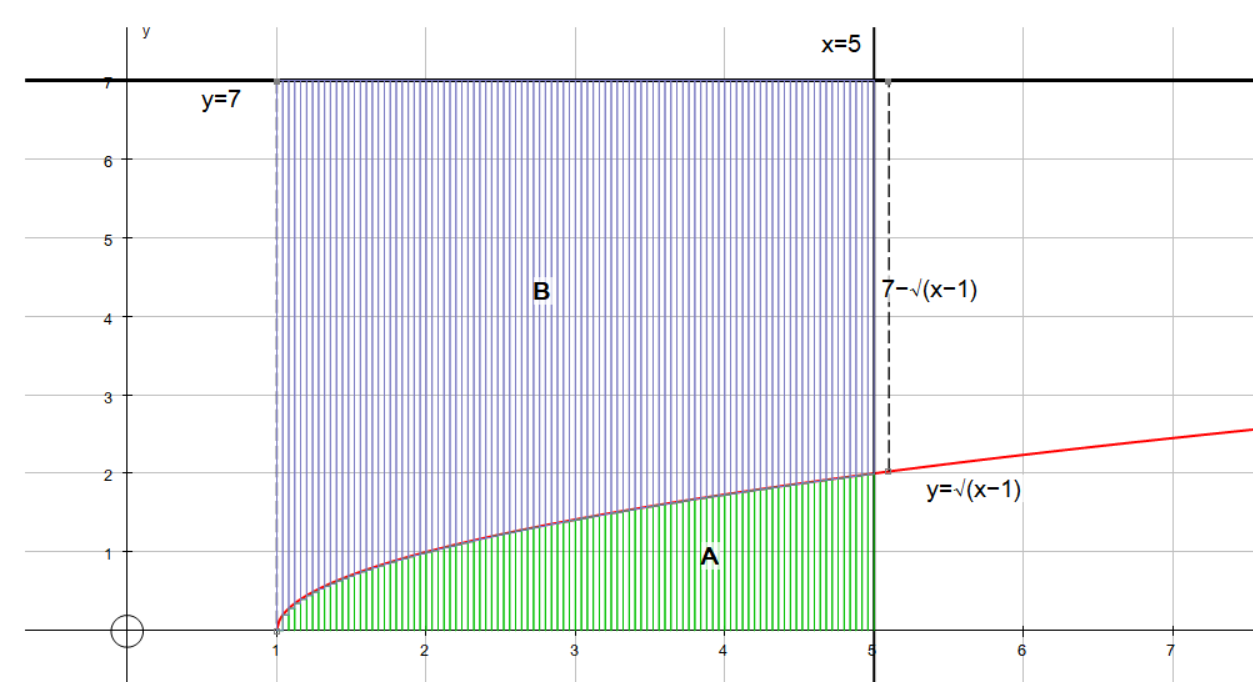
Looking at the graph, we can see that the area A rotated around
We can find this volume by finding the volume of the area (A+B). This is easy and doesn’t require integration. The radius of the cylinder that will be formed has a radius of 7, this is just the height from the x axis. We square this and multiply by
Length of interval is
Volume (A + B ):
From this we need to subtract the volume of B. From the graph we can see that the radius is
Volume of B:
Area first:
..................................................................................................................................
Volume=
Volume of A:
Volume of revolution: