How do you find the volume of the solid obtained by rotating the region bounded by the curves #f(x) = 3x^2# and #f(x) = 5x+2 # about the x axis?
1 Answer
Aug 20, 2015
Explanation:
The region bounded by the two functions, a vertical parabola and a straight line is shown in the picture. On solving the two equations the points of intersection can be easily found to be
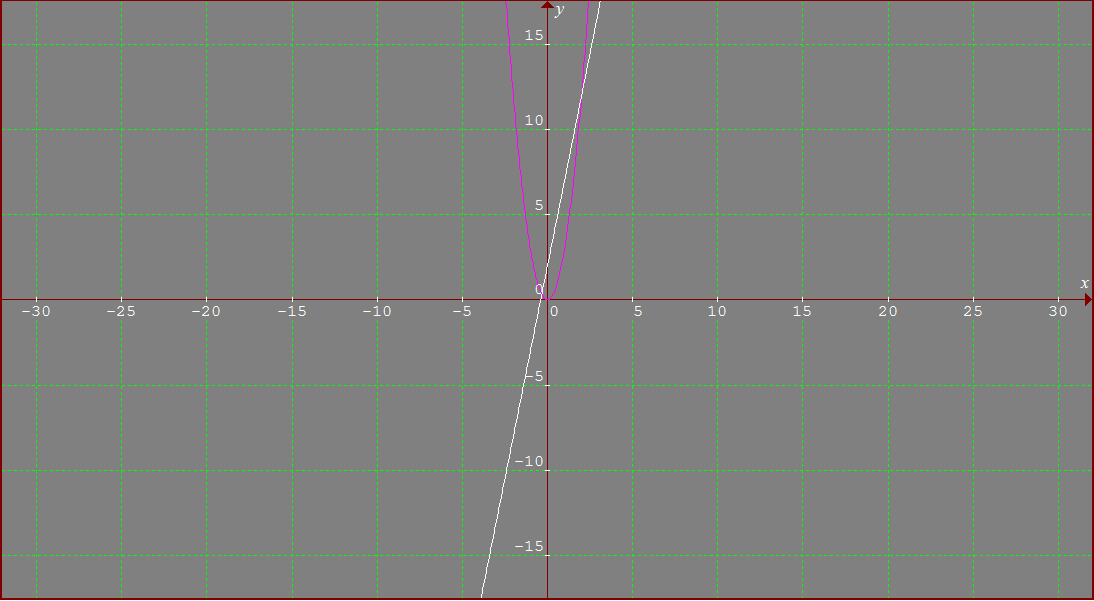
If
The volume of the solid formed by rotation of the whole region, about x axis would be
On solving, this integral would work out to be=
