How do you find the volume of the solid obtained by rotating the region bounded by the curves #x=y# and #y=sqrtx # about the line #x=2#?
1 Answer
Please see below.
Explanation:
Here is a graph of the region.
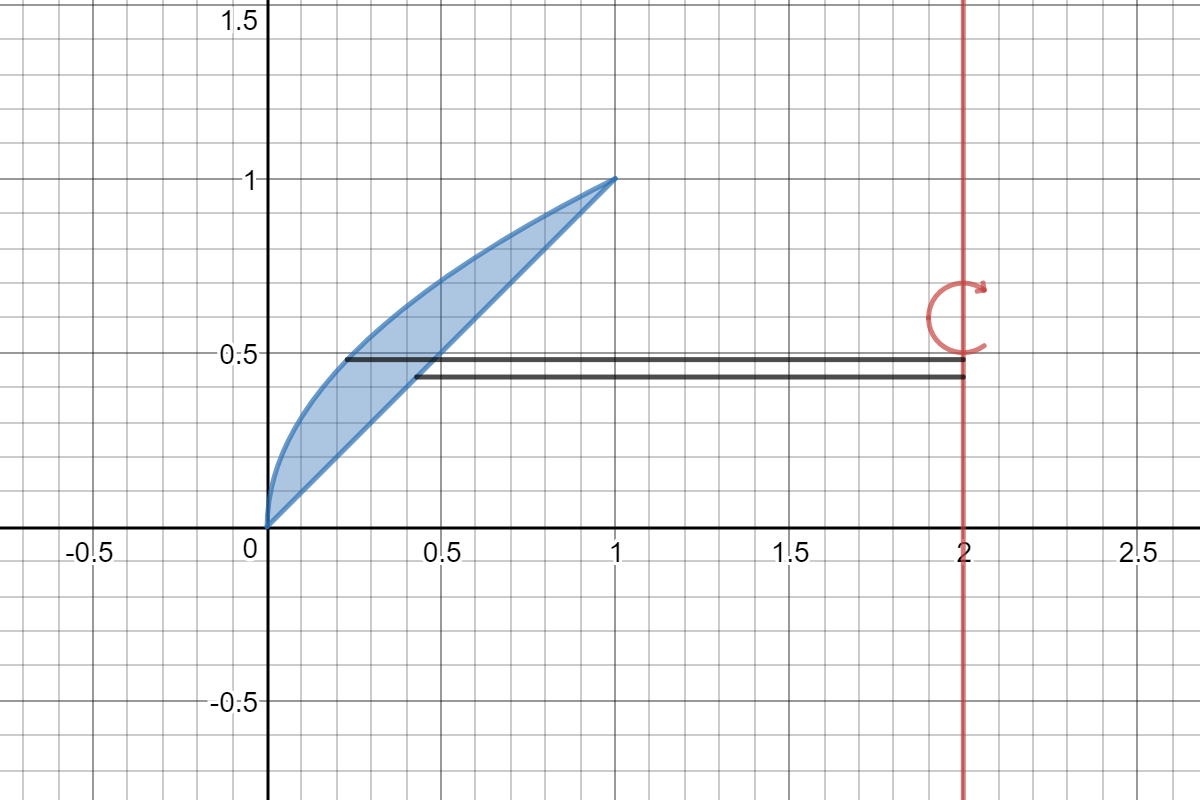
I've taken a slice perpendicular to the axis of rotation. The slice is taken at a variable value of
The thickness of the slice is
The curve on the left (
on the right is the line
Rotating the slice will generate a washer of thickness
volume
where
The outer radius of the washer is the distance between the curve on the left and the line
So
The inner radius is the distance from the line on the right and the line
So
The volume of the representative washer is
evaluate to get
# = pi (8/15) = (8pi)/15#

