How do you find the volume of the solid obtained by rotating the region bounded by the curves #f(x)=3x^2# and #g(x)=2x+1 # about the x axis?
1 Answer
Jul 4, 2015
I found:
Explanation:
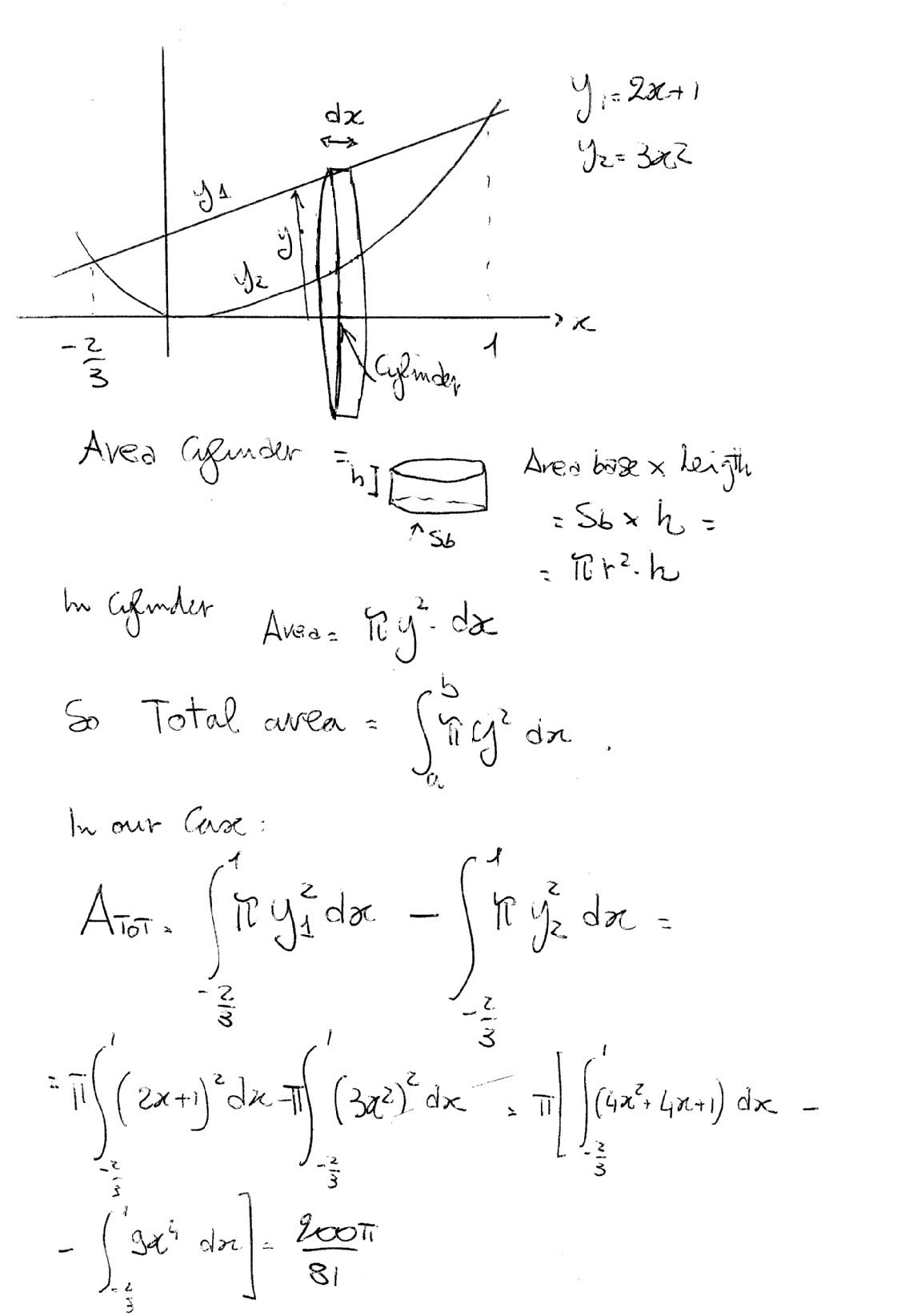
First let us see the area that will be rotated:
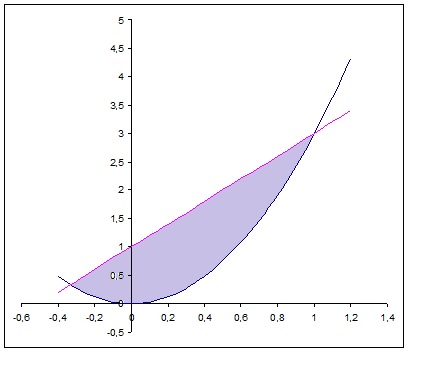
the two graphs meet at
We can use the "Cylinder" method to evaluate the volumes of the solid generated by the first function (line) and then subtract the volume of the second (parabola) as: