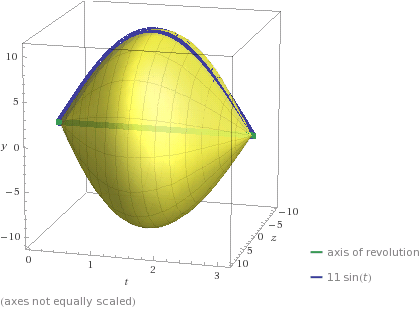
How do you find the volume of #y = 11sinx# , #y=0#, #[ 0,pi ]# revolving about the x axis?
1 Answer
Jun 10, 2015
Explanation:
This is the formula for calculating the volume of a solid obtained from a revolution around the x-axis:
Our function
So the volume is: