How do you find the volume of #y=3/(x+1)#, #y=0#; #x=0#; #x= 8# rotated around the x-axis?
1 Answer
Mar 30, 2016
Explanation:
The region to be rotated around x axis is shown, shaded blue, in the picture shown below
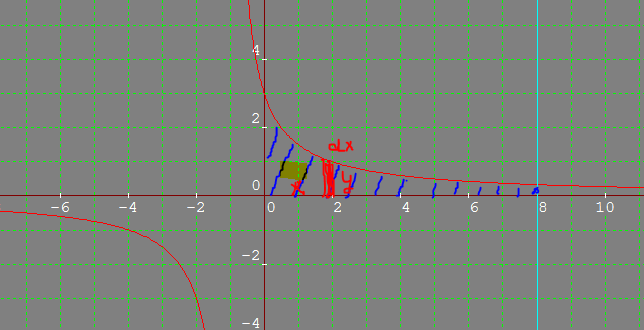 . In this region consider an element of width dx, at a distance x from y axis. Its length is y. If it is rotated about x axis, the volume of this elementary disc would be
. In this region consider an element of width dx, at a distance x from y axis. Its length is y. If it is rotated about x axis, the volume of this elementary disc would be
The volume of the solid so generated by the rotation of the whole shaded region would be
=
=
