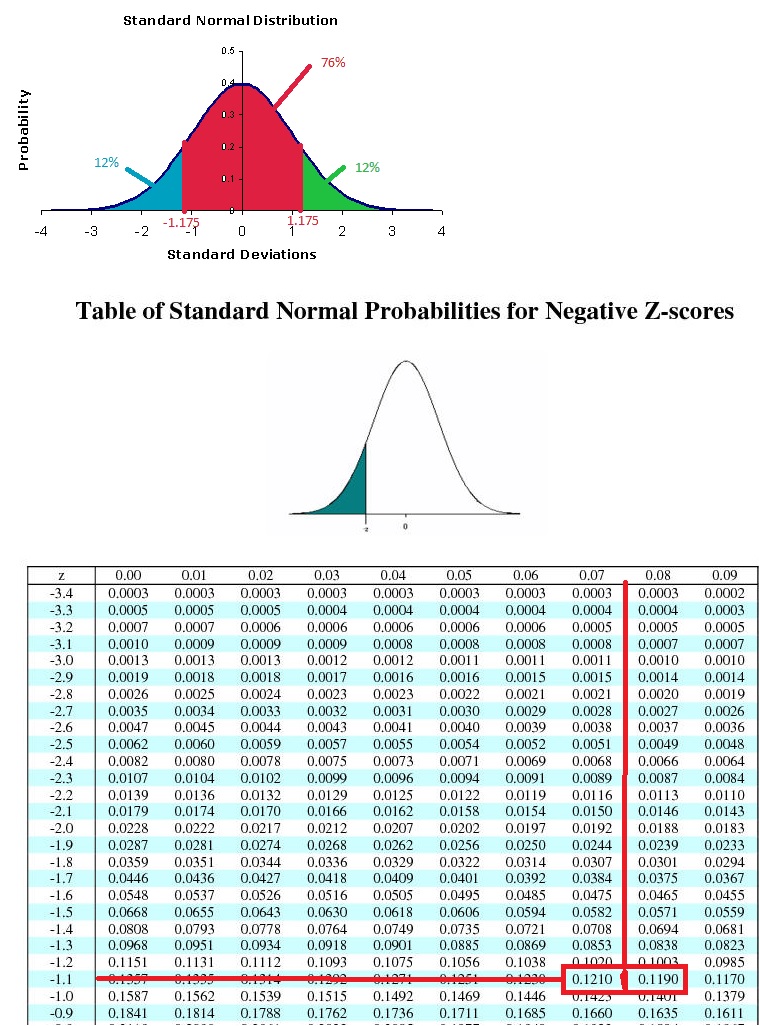
How do you find the z-score for which 76% of the distribution's area lies between -z and z?
1 Answer
May 18, 2015
Firstly in this question, we need to solve for
we can do this with the sum:
as
we also know that our Standard Normal Distribution is symmetric, so we must divide that
then we find a correlating
and we get that
This becomes easier to understand when visualized, so observe how we do this sum.