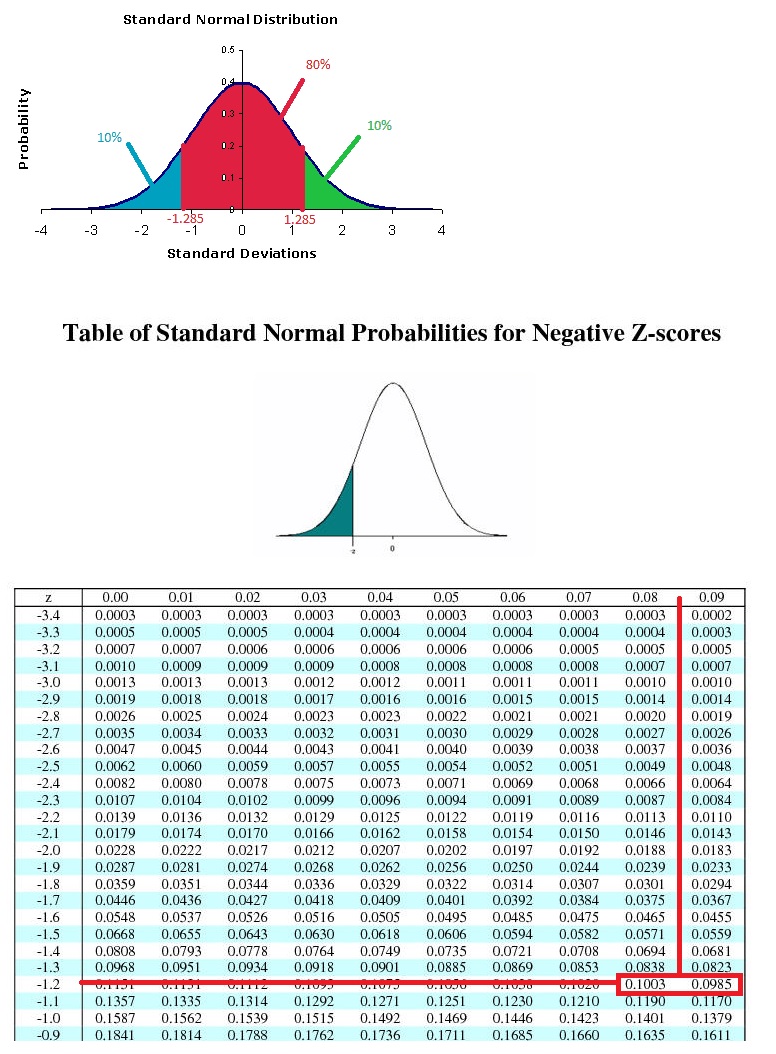
How do you find the z-score for which 80% of the distribution's area lies between -z and z?
1 Answer
May 19, 2015
Firstly we need to find
we also know that our Standard Normal Distribution is symmetric, so we would like to divide the area we don't want to be on either side of our area, so we solve for:
now it becomes easy to solve for
Which gets us:
This is easier do do if you draw it out: