How do you find values of t in which the speed of the particle is increasing if he position of a particle moving along a line is given by #s(t)=2t^3-24t^2+90t+7# for #t≥0#?
1 Answer
Feb 17, 2015
If
The speed (at time t) is given by
Acceleration is given by the second derivative
Critical point for acceleration (when the speed changes from decreasing to increasing) occurs when
That is when
This might be easier to see if we consider a table of time(t) and speed at time t:
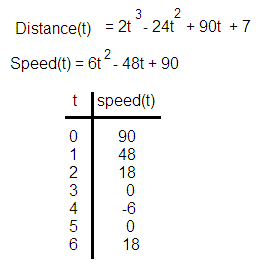
We can see that the speed actually decreases until somewhere between
