How do you find vertical asymptote of tangent?
1 Answer
Aug 27, 2014
I assume that you are asking about the tangent function, so
Recall that
#theta=pi/2+n pi, n in ZZ# in radians or
#theta=90+180n, n in ZZ# for degrees.
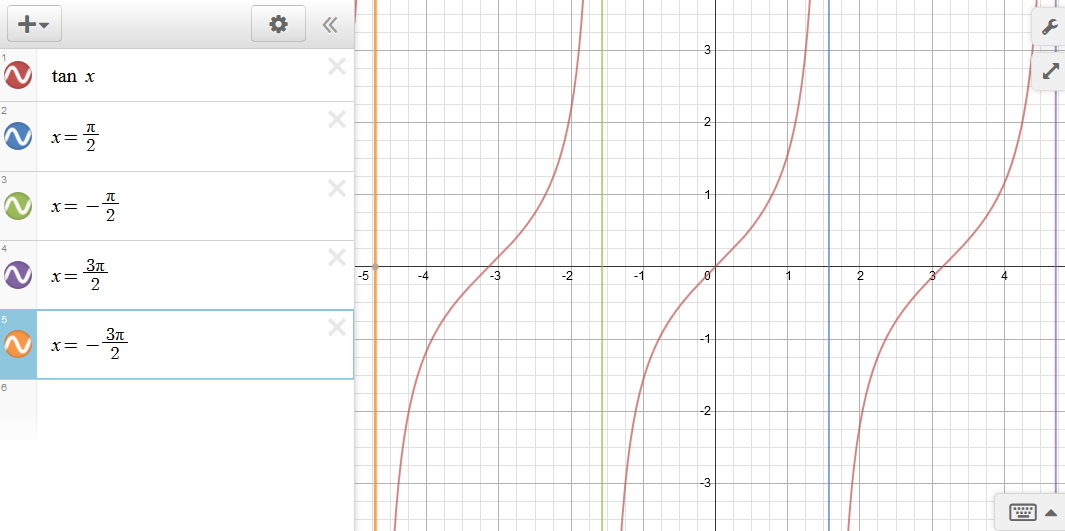
To find the vertical asymptote of ANY function, we look for when the denominator is 0.

