How do you find YX given #X=[(4,1), (-2,6)]# and #Y=[(0,-3)]# and #Z=[(-1,3), (0,-2)]#?
1 Answer
Explanation:
We are asked to find the matrix product
The process of matrix multiplication has us multiply each row of the first matrix by each column of the second matrix, multiplying each corresponding element and summing the results. This sum then goes into the element of the result which is at the row number of the selected row, and the column number of the selected column.
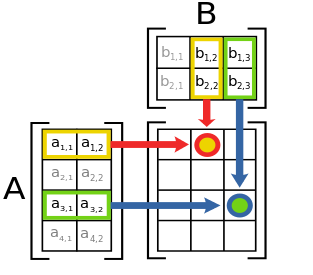
Starting with the first row (the only row!) times the first column:
Then the first row with the second column:
Finally

