How do you graph #-2|x+5|+4=2#?
2 Answers
The solution to this equation is two possible
Explanation:
The solution to this equation is two possible
Then add
Now we see that the quantity inside the absolute value signs must have a magnitude of
so the two solutions are
graphing this we get two points on the
graph{0=(y^2+(x+6)^2-0.02)(y^2+(x+4)^2-0.02) [-10, 10, -5, 5]}
In support of David's solution I have added a graph showing the actual function.
Explanation:
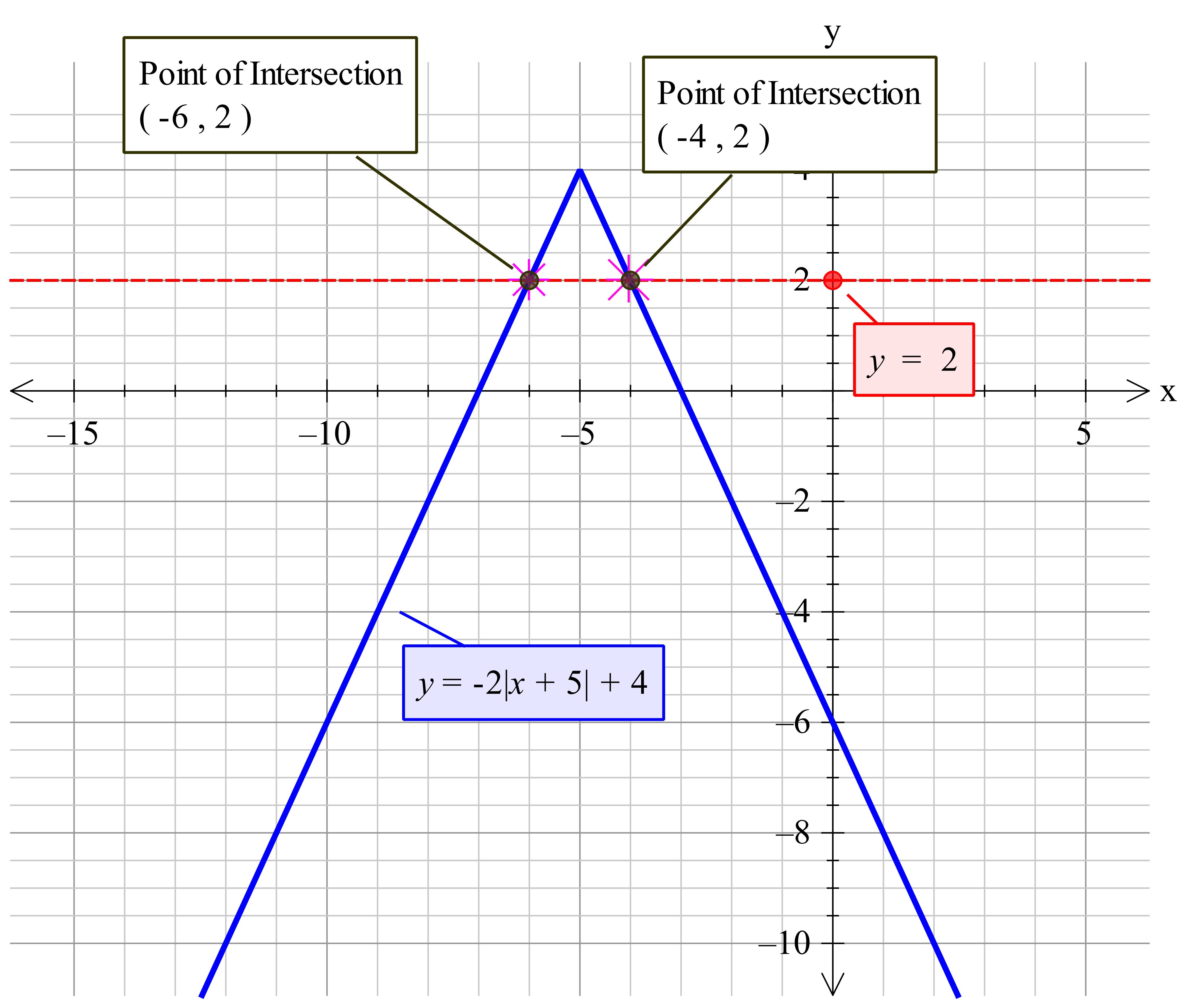
The values David give are consequential to the point of intersection of


