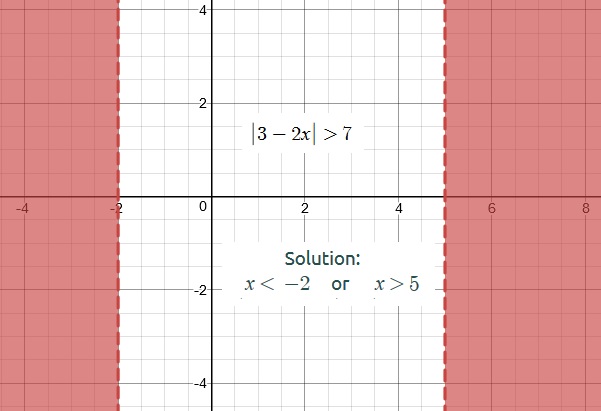
How do you graph and solve # |3-2x|>7#?
1 Answer
Solution:
Using Interval Notation:
Explanation:
Given the Inequity Expression:
We must remember that,
Hence,
we consider two possibilities as shown below:
First, we will consider
Subtract 3 from both sides
Simplify to get
Multiply both the sides by
We must remember to reverse the inequality
Simplify to get
Divide both sides by the value of
Next, we will consider
Subtract the value of 3 from both sides
Multiply both the sides by
We must remember to reverse the inequality
Divide both sides by the value of 2
Let us now combine both the intermediate results (1) & (2) to get
Using the Interval Notation we can can also write the solution as
Please refer to the inequality graph below which demonstrates our solution: