How do you graph and solve # |4x + 1| >= 5#?
1 Answer
Use the definition of the absolute value function:
to write two inequalities.
Simplify the restrictions.
Solve both inequalities.
Graph.
Explanation:
Given:
Use the definition of the absolute value function to write two inequalities:
Simplify the restrictions.
Solve the inequalities:
Because the inequalities do not violate the restrictions, we can drop them:
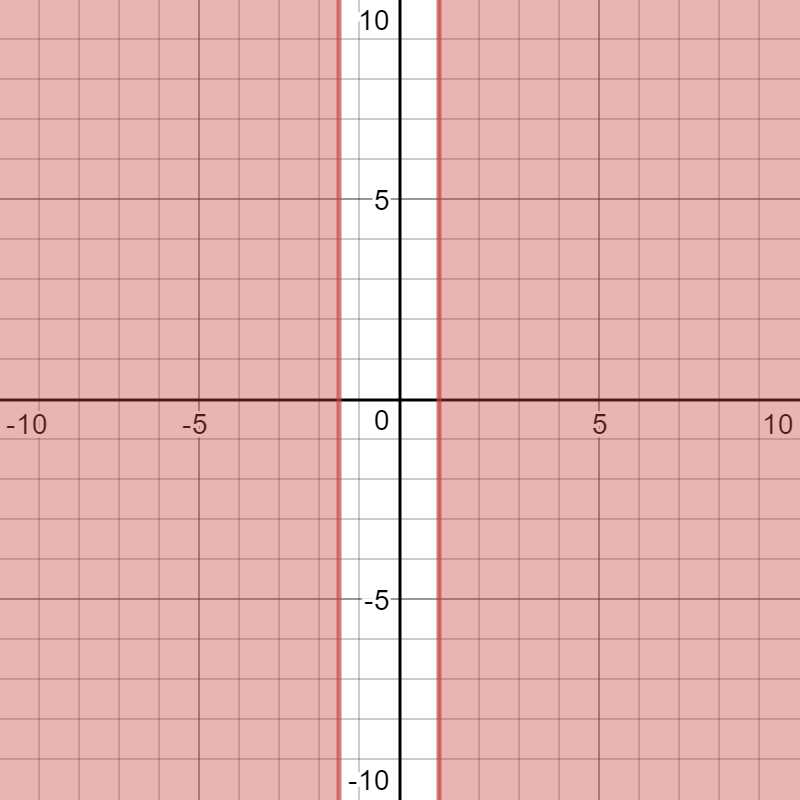
To graph the first inequality you draw a solid vertical line at
On the same graph, represent the second inequality by drawing a solid vertical line at
Here is that graph: