How do you graph and solve # abs(x + 4)<= -3#?
1 Answer
There are no solutions in
Explanation:
So, let's start with graphing.
The graph of
graph{|x| [-10.21, 9.79, -2.76, 7.24]}
It has the "peak" at
To graph
so the whole graph is basically shifted
graph{|x+4| [-10.21, 9.79, -2.76, 7.24]}
Now, the graphical representation of the inequality
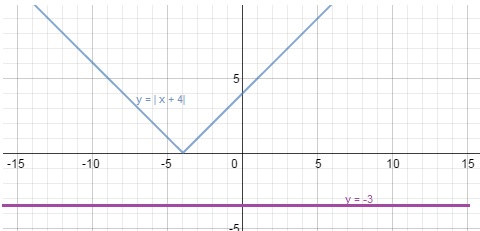
So, in my image those would be all the intervals where the blue graph is below the purple one.
As you can see, there are none, since the absolute value of any real number is always

