How do you graph, find any intercepts, domain and range of #f(x)=(1/4)^(x+4)-3#?

Question

1360 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-03T13:59:36

See below.

y axis intercept occurs when #x=0#

#y=(1/4)^(0+4)-3=1/256-3=color(blue)(-767/256)#

x axis intercept occurs when #y=0#

#(1/4)^(x+4)-3=0#

#(1/4)^(x+4)=3#

#(x+4)ln(1/4)=ln3=>x=(ln3)/(ln(1/4))-4~~color(blue)(-4.792)#

There are no constraints on #x# so domain is:

#color(blue)({x in RR})#

as #x->oo# , #color(white)(888)(1/4)^(x+4)->0#

So:

as #x->oo# , #color(white)(888)(1/4)^(x+4)-3->-3#

The line #color(blue)(y=-3) color(white)(88)# is a horizontal asymptote.

For #x<-4#

#(1/4)^(x+4)# becomes #color(white)(888)1/((1/4)^(x+4))#

So:

as #x->-oo# , #color(white)(888)1/((1/4)^(x+4))->oo#

and:

#x->-oo# , #color(white)(888)1/((1/4)^(x+4))-3->oo#

#color(blue)({y in RR : -3 < y < oo })#

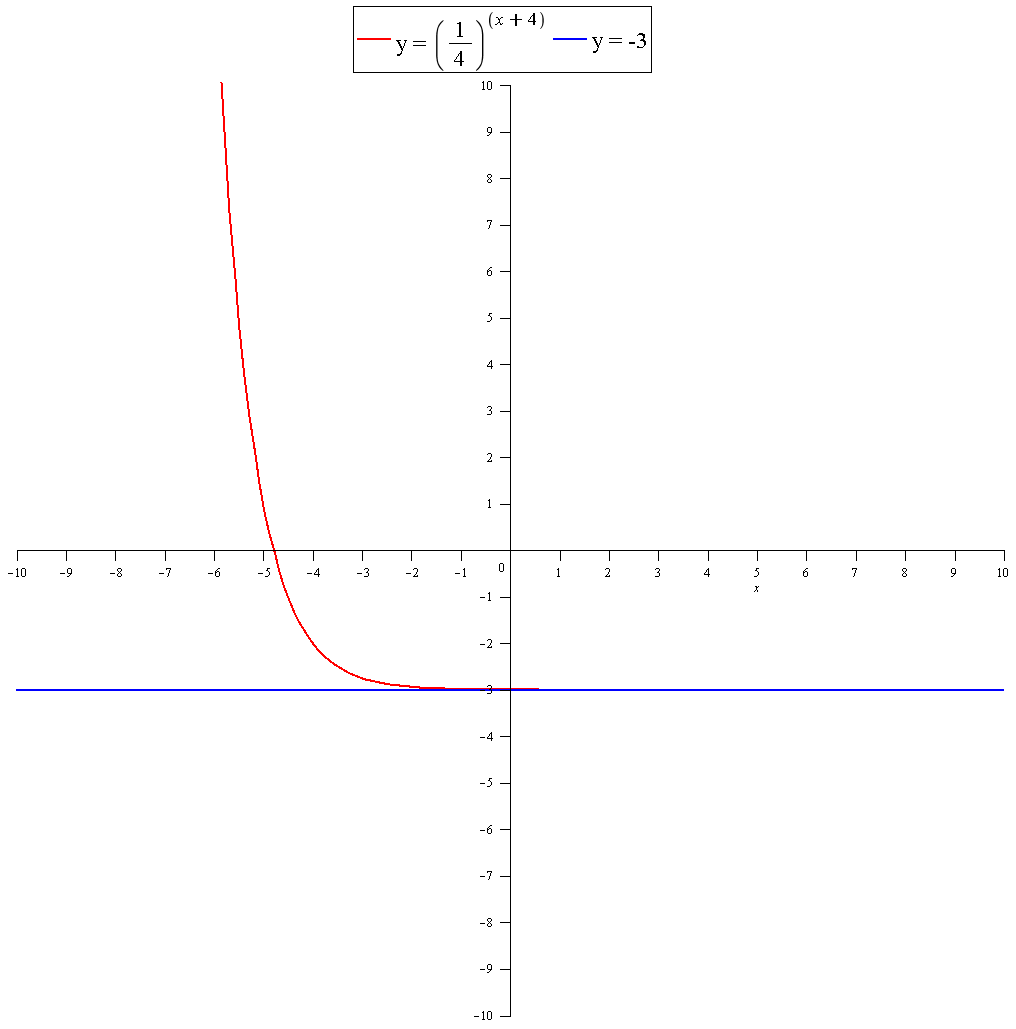
Graph:

enter image source here