Question

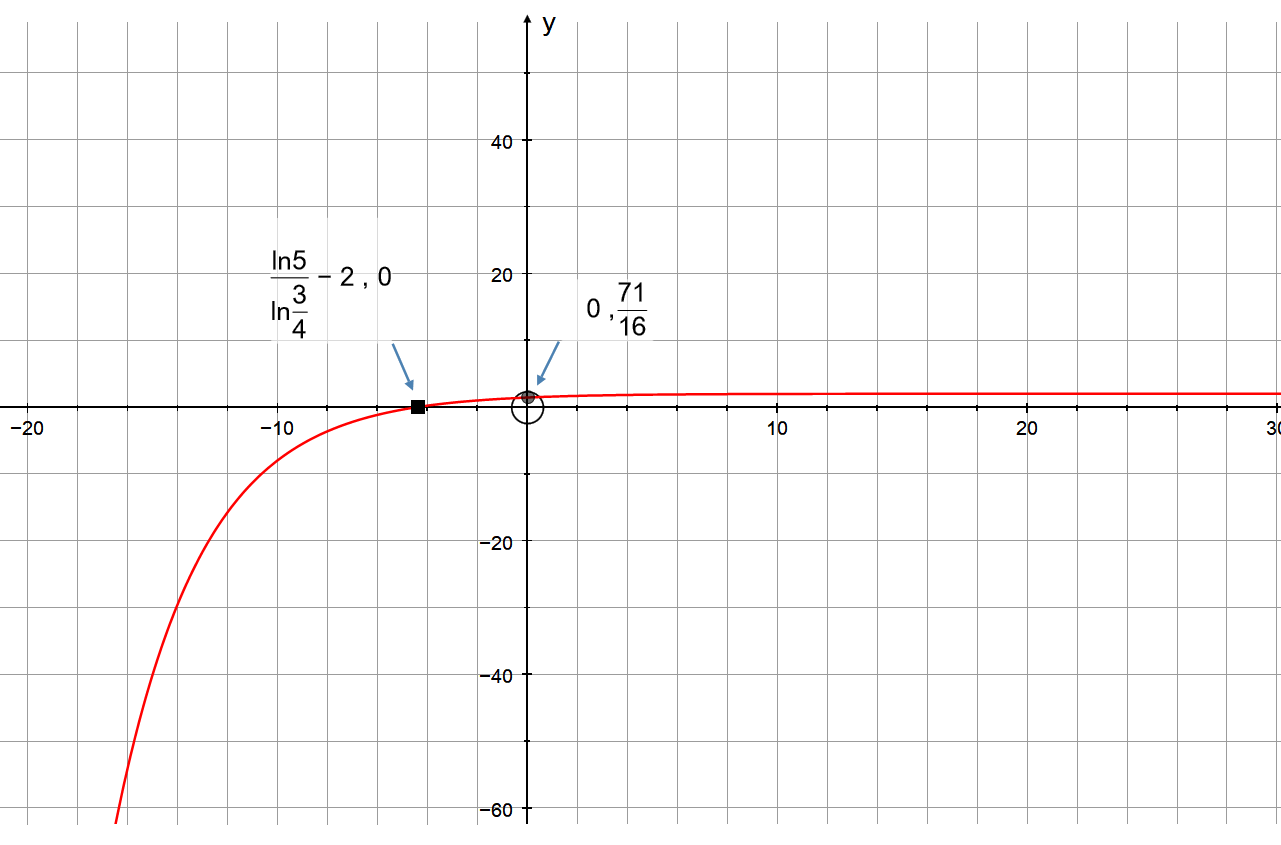
How do you graph, find any intercepts, domain and range of `f(x)=-(3/4)^(x+2)+5`?

Answer 1

See below.

Explanation:

`f(x)=-(3/4)^(x+2)+5`

`y` axis intercepts occur where `x=0`

`y=-(3/4)^(0+2)+5=-(3/4)^2+5=-9/16+5=color(blue)(71/16)`

`x` axis intercepts occur where `y=0`

`-(3/4)^(x+2)+5=0`

`(3/4)^(x+2)=5`

Taking logarithms of both sides:

`(x+2)ln(3/4)=ln(5)`

`x=color(blue)((ln(5))/(ln(3/4))-2)`

There are no restriction on `x`, so the domain is:

`{x in RR}`

To find the range we need to see what happens as `x` approaches `+-oo`

as `x->oo`, `\ \ \ \ \-(3/4)^(x+2)+5 -> 5`

as `x->-oo`, `\ \ \ \ \-(3/4)^(x+2)+5 -> -oo`

So the range is:

`{y in RR : 5 < y < oo}`

The graph confirms these findings: