Graph #f(x) = | 2x |# piecewise:
Notice that #f(x) = |2x|# is equivalent to #f(x) = 2x# for #x >=0#
and #f(x) = -2x# for #x <= 0# ,because the absolute value is always positive.
The graph will look like this:
graph{|2x| [-22.8, 22.8, -11.4, 11.4]}
The function #f(x) = |2x|# maps two elements in the domain to one element in the range:
example: #-2# and #2# both map to #4#.
The inverse would then need to map #4# onto both #-2# and #2# . This is a one many relationship, and is therefore NOT A FUNCTION. However inverse functions can be found by restricting the domain of the function:
Example: #f(x) = |2x|# for domain #{x in RR^+}#
would have #f^-1(x) = (x/2)#
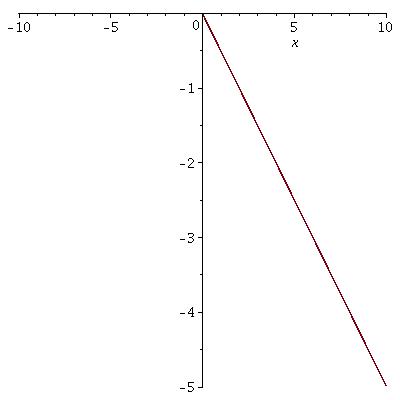
And: #f(x) = |2x|# for domain #{x in RR^- }#
would have #f^-1(x) = -(x/2)#
graph:
Inverse for domain #RR^+#
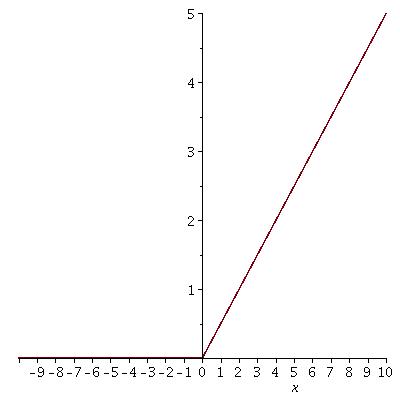
Inverse for domain #RR^-#