Transpose (manipulate) the equation as follows:
Add #color(blue)(5y)# to both sides
#color(brown)(2x-5ycolor(blue)(+5y)=10color(blue)(+5y))" "->" "2x+0=10+5y#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Subtract #color(blue)(10)# from both sides
#color(brown)(2xcolor(blue)(-10)=10color(blue)(-10)+5y)" "->" "2x-10=0+5y#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Divide both sides by #color(blue)(5)#
#color(brown)( (2x)/(color(blue)(5)) -10/(color(blue)(5)) = 5/(color(blue)(5)) xx x#
But #5/5=1#
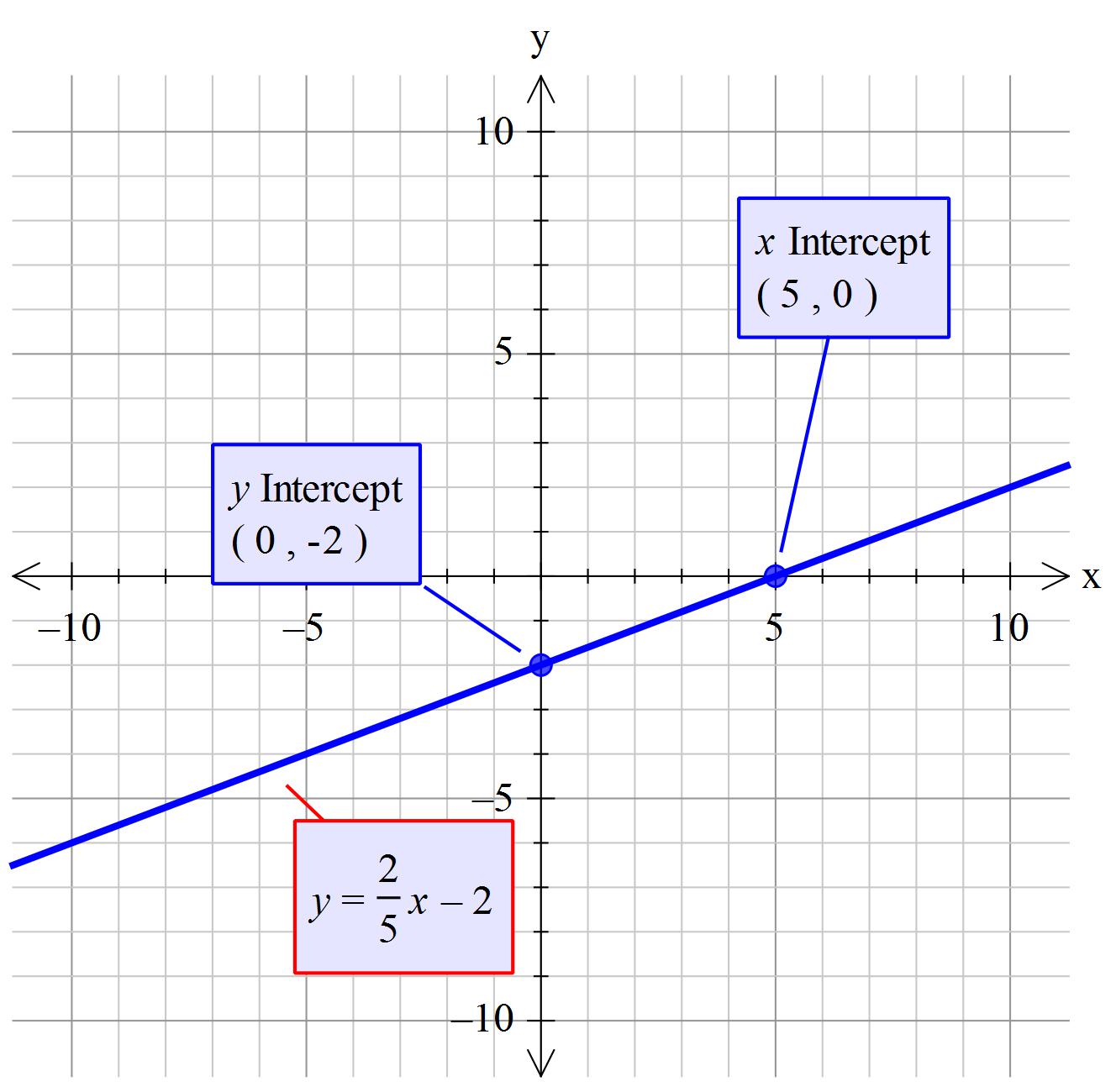
#color(blue)(y=2/5 x-2)" " #This is standard form of the equation
#color(red)("=================================")#
The line crosses the y-axis ( #y_("intercept"# ) when #x=0#
so #y_("intercept")= 2/5 (0)-2 = -2#
So one point is:#" "(x,y)->(0,-2)#
#color(red)("Mark that point on the graph")#
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The line crosses the x-axis ( #x_("intercept")# ) at #y=0#
#0=2/5 x-2#
#=> 2 xx5/2=x = 5#
So the other point is:#" "(x,y)->(5,0)#
#color(red)("Mark that point on the graph")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Draw a line through both these points and that is your graph.")#