How do you graph #y=-4(x+2)^2-1#?
1 Answer
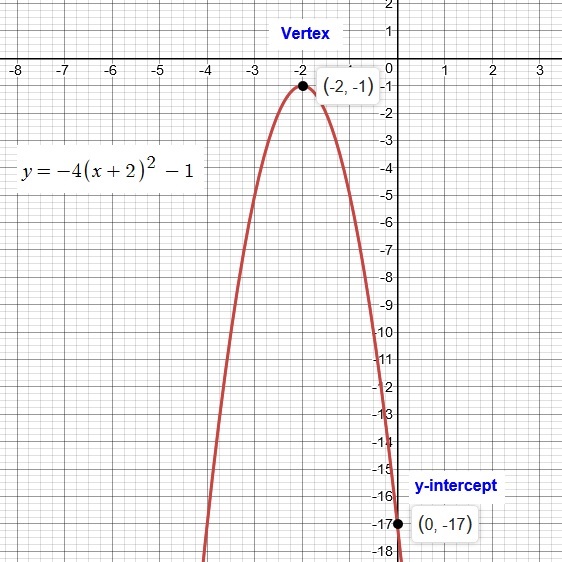
Vertex
Axis of Symmetry
Coefficient of
Hence. the parabola opens down.
y-intercept:
Explanation:
We are given the function
Note.A:-
Standard Form:
Note.B:-
Vertex Form:
Vertex Form represents the Parabola
Note.C:-
Axis of Symmetry:
Note.D:-
In the Standard Form, if the coefficient of
In the Standard Form, if the coefficient of
Note.E:-
If the parabola opens up, we have a Minimum
If the parabola opens down, we have a Maximum
From now on, we will analyze our problem:
We are given the function
Since the coefficient of the
the parabola opens down.
In our problem, with reference to the Vertex Form,
Vertex
Axis of Symmetry:
To find the y-intercept substitute the value
Hence, the y-intercept is at:
Please refer to the graph below: