.
#-(11pi)/4# is a negative angle. In standard position, the initial side of the angle lies on the positive #x#-axis and the angle opens clockwise. Every time the terminal side of the angle sweeps through the entire unit circle and reaches its starting point, the angle has opened by #-2pi# radians.
#-(11pi)/4=-(8pi)/4-(3pi)/4=-2pi-(3pi)/4#
This means the angle opens clockwise from its initial position on the positive #x#-axis, makes a full circle and passes through its starting point, and continues to open another #-(3pi)/4#.
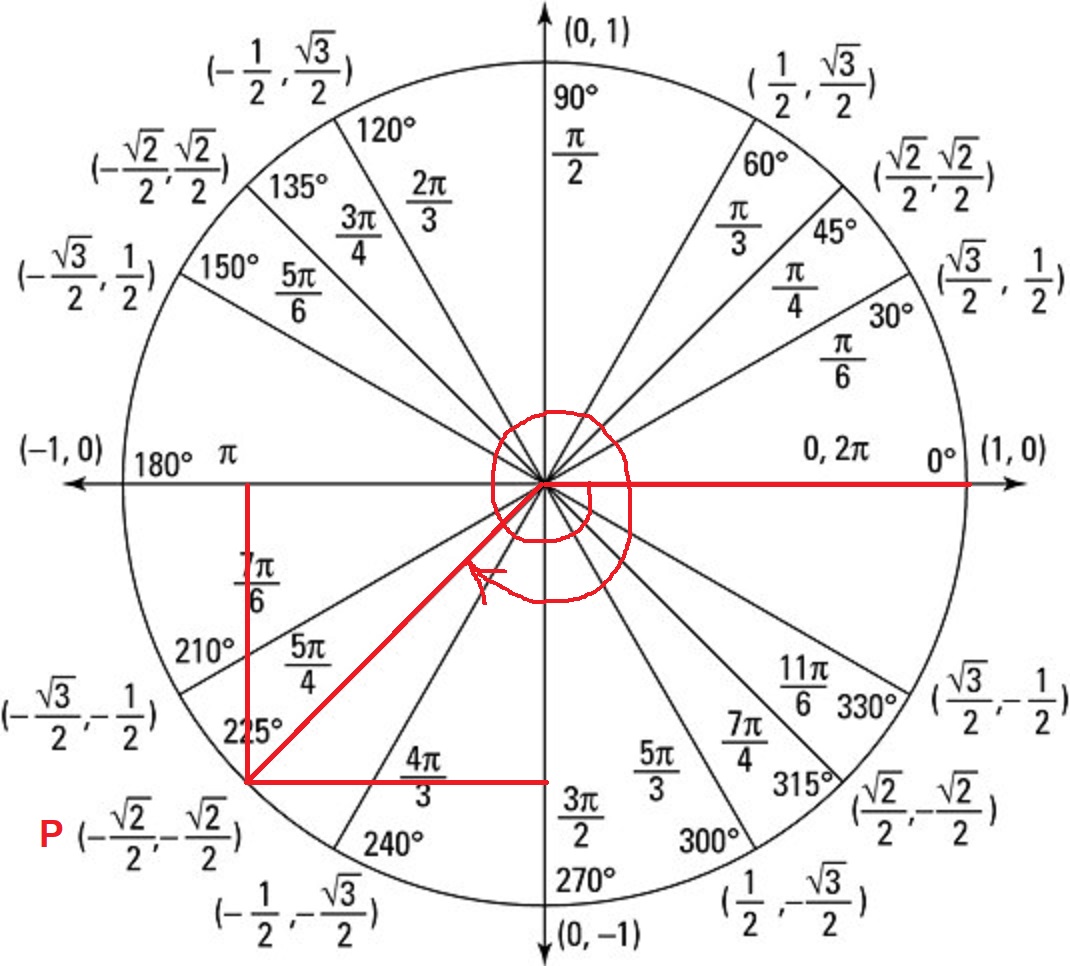
This puts the terminal side of the angle at #-pi/4# past the #y#-axis.
The positive co-terminal angle with #-(11pi)/4# wou;d be #(5pi)/4# which would share its terminal side with this angle as shown below:
Therefore, point #(x,y)# is:
#P (-sqrt2/2, -sqrt2/2)#