How do you integrate?
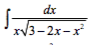
1 Answer
Use the substitution
Explanation:
Let
#I=intdx/(xsqrt(3-2x-x^2))#
Complete the square in the square root:
#I=intdx/(xsqrt(4-(x+1)^2))#
Apply the substitution
#I=int(4cos2thetad theta)/((2sin2theta-1)(2cos2theta))#
Simplify:
#I=2int(d theta)/(4sinthetacostheta-1)#
Rearrange:
#I=2int(sec^2thetad theta)/(4tantheta-sec^2theta)#
Apply the identity
#I=2int(sec^2thetad theta)/(4tantheta-tan^2theta-1)#
Complete the square in the denominator:
#I=2int(sec^2thetad theta)/(3-(tantheta-2)^2)#
Apply the difference of squares
#I=2int(sec^2thetad theta)/((sqrt3+tantheta-2)(sqrt3-tantheta+2))#
Apply partial fraction decomposition:
#I=1/sqrt3int(1/(sqrt3+tantheta-2)+1/(sqrt3-tantheta+2))sec^2thetad theta#
Integrate directly:
#I=1/sqrt3{ln|sqrt3+tantheta-2|-ln|sqrt3-tantheta+2|}+C#
Combine terms:
#I=1/sqrt3ln|(sqrt3+tantheta-2)/(sqrt3-tantheta+2)|+C#
Rearrange:
#I=1/sqrt3ln|(sqrt3+tantheta-2)/(sqrt3-tantheta+2)*(sqrt3-tantheta+2)/(sqrt3-tantheta+2)|+C#
Simplify:
#I=1/sqrt3ln|(3-(tantheta-2)^2)/(sqrt3-tantheta+2)^2|+C#
Rearrange:
#I=1/sqrt3ln|(3-(tantheta-2)^2)/(sqrt3-tantheta+2)^2*cos^2theta/cos^2theta|+C#
Simplify:
#I=1/sqrt3ln|(2sin2theta-1)/((2+sqrt3)costheta-sintheta)^2|+C#
Separate terms:
#I=1/sqrt3ln|2sin2theta-1|-1/sqrt3ln|((2+sqrt3)costheta-sintheta)^2|+C#
Expand:
#I=1/sqrt3ln|2sin2theta-1|-1/sqrt3ln|(2+sqrt3)^2cos^2theta+sin^2theta-2(2+sqrt3)^2sinthetacostheta|+C#
Rescale
#I=1/sqrt3ln|2sin2theta-1|-1/sqrt3ln|((2+sqrt3)^2cos^2theta+sin^2theta-2(2+sqrt3)sinthetacostheta)*(4-2sqrt3)|+C#
Simplify:
#I=1/sqrt3ln|2sin2theta-1|-1/sqrt3ln|4+2sqrt3(cos^2theta-sin^2theta)-4sinthetacostheta|+C#
Apply the double-angle trigonometric identities:
#I=1/sqrt3ln|2sin2theta-1|-1/sqrt3ln|4+2sqrt3cos2theta-2sin2theta|+C#
Reverse the substitution:
#I=1/sqrt3ln|x|-1/sqrt3ln|sqrt(9-6x-3x^2)-x+3|+C#
