How do you integrate A and B?
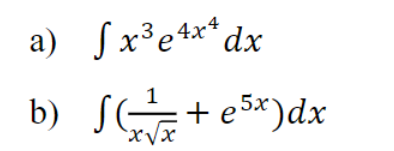
2 Answers
Given:
Let
Reverse the substitution:
Given:
Substitute
Separate into two integrals:
The first integral fits the power rule and the second integral is well known:
Explanation:
Part (a) :
Let,
Note that,
Part (b) :
Suppose that,
Here, we use,
Spread the Joy of Maths.!
