How do you integrate #int x^3e^x# by integration by parts method?
1 Answer
Using integration by parts:
Explanation:
The equation for integration by parts is this:
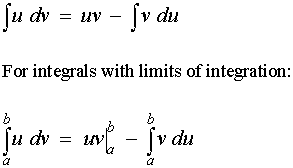
I think mathematicians use similar letters on purpose to confuse people. Thats why they chose
Anyways, we have to pick our
let
That leaves the rest of the integral to be
let
To recap, so far, we have
#u = x^3# #du = 3x^2dx# #dv = e^xdx# #v = e^x#
so
So lets go again!
#u = 3x^2# #du = 6xdx# #dv = e^xdx# #v = e^x#
So lets go again (because calculus is so fun)!
#u = 6x# #du = 6dx# #dv = e^xdx# #v = e^x#
Simplify
Then you can take out the
Don't forget to add + C at the end, to signify that there is a group of equations what this integral could be.

