How do you know when a linear regression model is appropriate?
1 Answer
When it fits four assumptions : homogeneity, normality, fixed X and independence of the variables
Explanation:
-Before applying your model
Checking for fixed X:
You should know the exact value of X before your analysis. In other words, the uncertainty on X has to be the lowest as possible. for example, you cannot take age as an explanatory variable if the lifespan is 25 years and you have an uncertainty of 3 years.
Checking for independence :
In the case of a multivariate linear regression, your explanatory variables have to be independent. In other words, do not use colinear variables in the same model.
To check this, plot one variable against the other. If you detect a strong linear or non linear pattern, they are dependent.
- Once you have applied your model
Checking for normality :
The residuals of your model (the variance not explained by your model) have to follow a normal distribution.
You can check this by an histogram of the residuals or by a quantile-quantile plot.
You can see on the graphs below how it should looks like when you have normality.
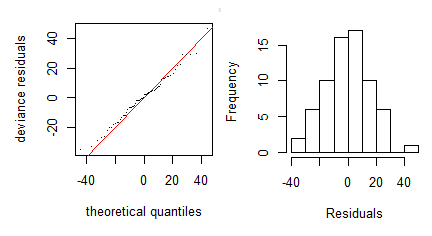
However, normality is not the most important assumption and linear models are robust enough to a small amount of non-normality.
Checking for homogeneity:
This assumption is much more important. To check it, you can plot the residuals of your model against the fitted values.
You have homogeneity when the spread is more or less the same for all the residuals (you do not see any particular pattern, see figure below).
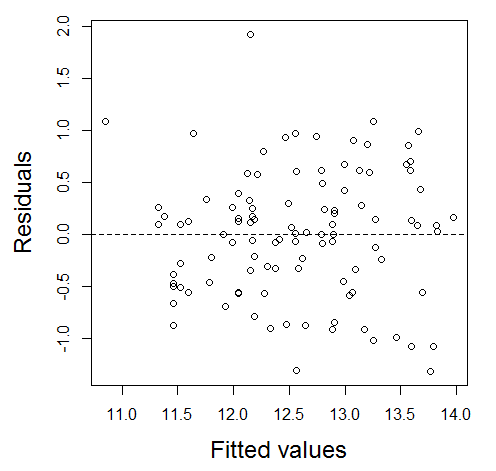
If your residuals show a pattern (linear or non linear) or have a cone shape (spread higher in one side of the graph and lower at the other side), this assumption is not supported and you should find another kind of model.
You should do the same for each explanatory variable (X).

