How do you list all possible roots and find all factors of #x^5+7x^3-3x-12#?
1 Answer
Possible rational zeros are:
#+-1, +-2, +-3, +-4, +-6, +-12#
but none are actually zeros.
This quintic is not solvable using radicals and elementary functions.
Explanation:
Rational roots theorem
By the rational roots theorem, any rational zeros of
That means that the only possible rational zeros are:
#+-1, +-2, +-3, +-4, +-6, +-12#
Note that when
#abs(7x^3)+abs(3x)+abs(12) <= abs(7x^3)+abs(3x)+abs(4x) = abs(7x^3)+abs(7x) < abs(7x^3)+abs(x^3) = abs(8x^3) < abs(x^5)#
So no
Checking the other possible rational zeros, we find:
#f(-2) = -32-56+6-12 = -94#
#f(-1) = -1-7+3-12 = -17#
#f(1) = 1+7-3-12 = -7#
#f(2) = 32+7-6-12 = 21#
So
Quintic
In fact this is a typical quintic with
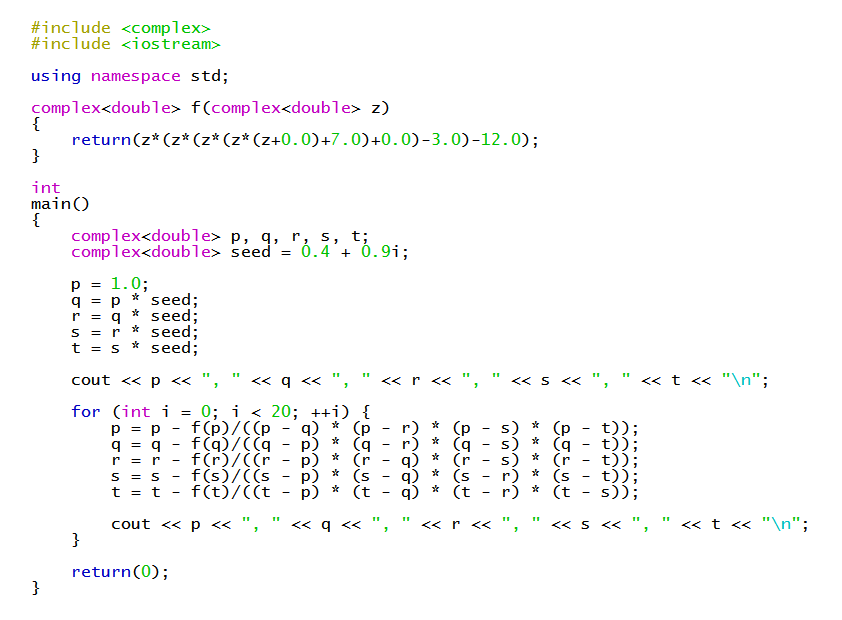
About the best you can do is find approximations using numerical methods such as Durand Kerner.
See https://socratic.org/s/aAGsRKkf for another example and a description of the Durand-Kerner algorithm for a quintic.
Using this algorithm, I found the following approximations:
#x_1 ~~ 1.22622#
#x_(2,3) ~~ 0.101096+-2.734i#
#x_(4,5) ~~ -0.714207+-0.892944i#
Here's the C++ program I used: