#(5-sqrt(-36))(3-sqrt(-25))#
First, let's simplify #sqrt(-36)#:
#sqrt(-36) = sqrt(-1) * sqrt36 = 6i# (#i# refers to an imaginary/complex number, meaning it is not real)
Then #sqrt(-25)#:
#sqrt(-25) = sqrt(-1) * sqrt25 = 5i#
Therefore, the expression is:
#(5-6i)(3-5i)#
To simplify this, we expand/simplify this using FOIL:
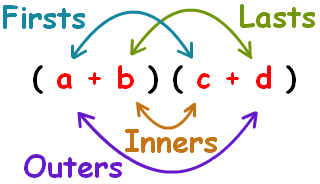
Following this image, we can multiply it out.
The #color(teal)("firsts")#:
#color(teal)(5*3) = 15#
The #color(indigo)("outers")#:
#color(indigo)(5 * -5i) = -25i#
The #color(peru)"inners"#:
#color(peru)(-6i * 3) = -18i#
The #color(olivedrab)"lasts"#:
#color(olivedrab)(-6i * -5i) = 30i^2#
We also know that #i^2# is the same thing as #-1#, so the expression becomes:
#30 * -1 = -30#
Combine them all together to get:
#15 - 25i - 18i - 30#
Color-code the like terms:
#color(red)(15) quadcolor(blue)(-quad25i) quadcolor(blue)(-quad18i) quadcolor(red)(-quad30)#
Combine like terms to get:
#-15 - 43i#
Hope this helps!


