How do you prove?
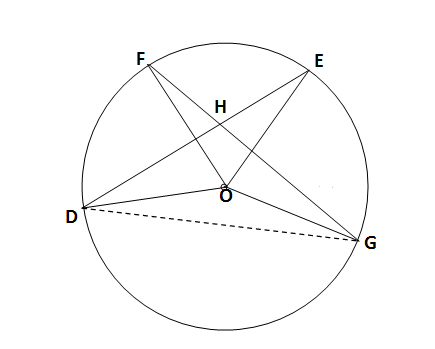
If a circle with centre O has two chords DE and FG which intersect at point H then prove that #/_DOF+/_EOG=2/_EHG# ?
If a circle with centre O has two chords DE and FG which intersect at point H then prove that
1 Answer
Dec 16, 2017
Given
A circle with centre O has two chords DE and FG which intersect at point H .
RTP
we are to prove that
Construction : D and G are joined.
Proof
Now the central
So
Similarly the central
So
Adding [1] and [2] we get
(exterior angle of a triangle is equal to sum of two of the remote interior angles of the triangle.)