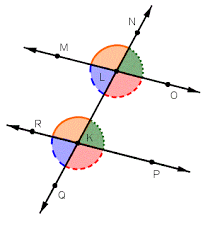
Let #MO# and #PR# be two parallel lines and #NQ# is a transverse, that, on the way from point #N# to point #Q#, intersects, first, line #MO# at point #L# and then line #PR# at point #K#. Points #P# and #O# lie on one side of transverse #PQ#, while points #M# and #R# are on the other side.
Two one-sided angles (on one side of transverse #NQ#), of which one is interior or inner (between the parallels) and another exterior (outside of the area between the parallel lines), are called corresponding.
So, angles #∠MLN# and #∠RKL# are corresponding, so are some other pairs, like #∠NLO# and #∠LKP# etc. as shown on the picture by the same color.
Take into account that sum of measures of supplemental angles #∠MLN# and #∠MLK# is #180^o#.
That is, #∠MLN + ∠MLK = 180^o# or
#∠MLN = 180^o - ∠MLK#
Now, if the corresponding angles #∠MLN# and #∠RKL# are not equal in measure, then sum of inner angles #/_MLK# and #/_RKL# would be either less or greater than #180^o# since #/_MLN != /_RKL# implies that #∠RKL != 180^o - ∠MLK# and, therefore, #∠RKL + ∠MLK != 180^o#.
There are two cases, both mean that a sum of some pair of inner angles measure less than #180^o#:
#∠RKL + ∠MLK < 180^o# or
#∠RKL + ∠MLK > 180^o#, in which case, obviously, the sum of the other pair of inner angles' measures is less than #180^o#:
#∠PKL + ∠OLK < 180^o#.
Let's recall the Fifth Postulate of Euclid.
If two lines on a plane intersect a third line in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
Therefore, since #∠RKL + ∠MLK != 180^o#, lines #MO# and #RP# are NOT parallel to each other, that contradicts the premise of the theorem.


