How do you prove #cos^2x=(cscx cosx)/(tanx+cotx)# ?

Question

15324 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-05T22:51:32

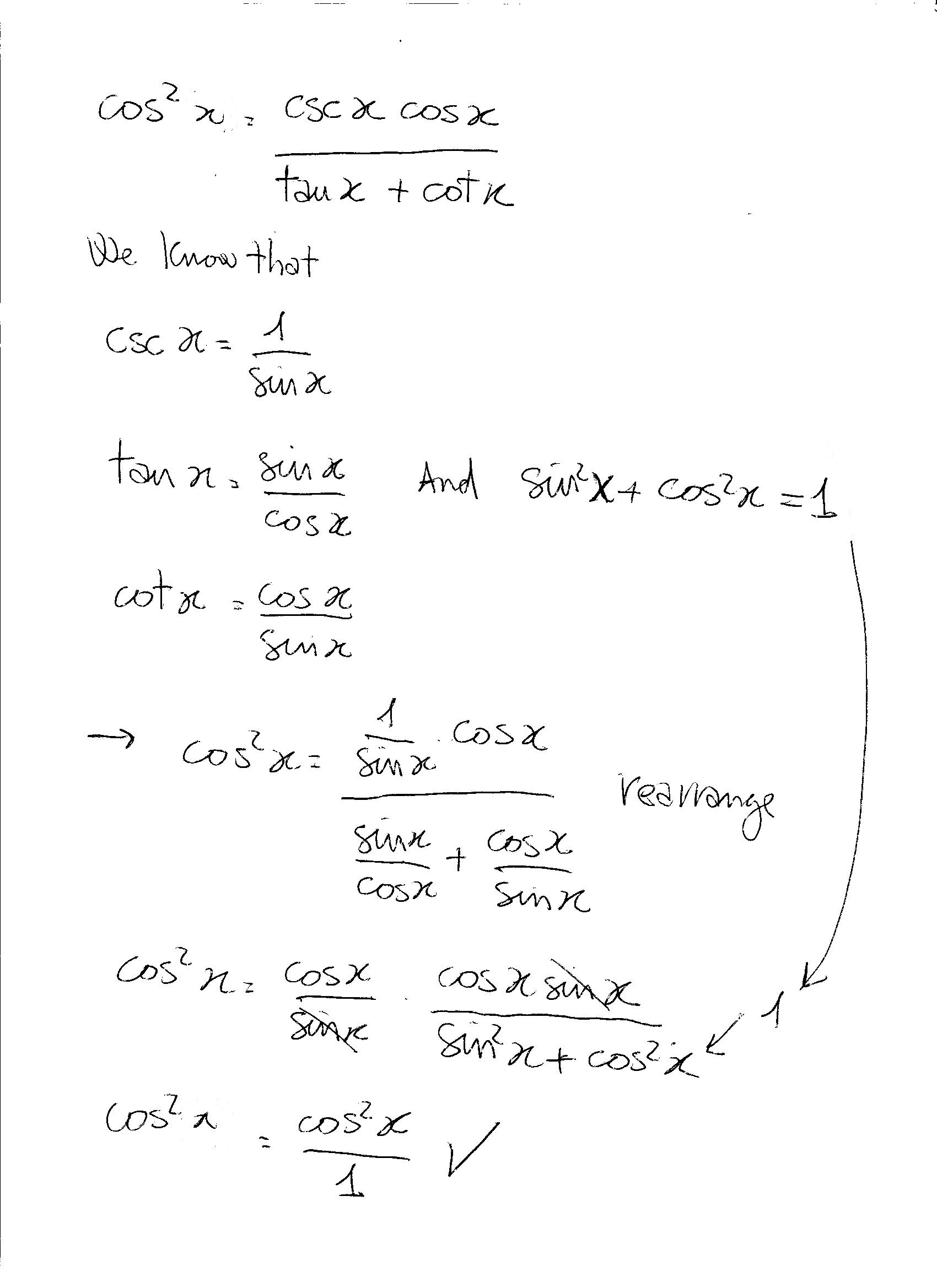
I tried this:

Have a look:

enter image source here

Answer 2 · 2018-03-05T22:57:16

See below.

Identities:

1) #color(red)bb(cscx=1/sinx)#

2) #color(red)bb(tanx=sinx/cosx)#

3) #color(red)bb(cotx=cosx/sinx)#

4) #color(red)bb(sin^2x+cos^2x=1)#

#RHS#

#(1/sinxcosx)/(sinx/cosx+cosx/sinx)#

Add fractions in the denominator:

#(cosx/sinx)/((sin^2x+cos^2x)/(cosxsinx))#

Using identity 4

#(cosx/sinx)/((1)/(cosxsinx))#

Multiply numerator and denominator by #cosxsinx#

#(cosxsinxcosx/sinx)/((cosxsinx)/(cosxsinx))#

#(cosxcancel(sinx)cosx/cancel(sinx))/1=cos^2x#

#RHS-=LHS#