How do you prove that đq is not an exact differential for an isobaric process using #đq = dU - đw# where the only work is PV work?
I understand that heat is a path function and this:
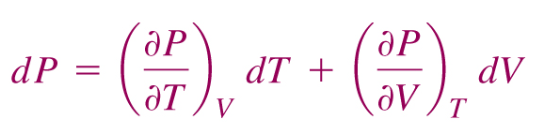
Where dP is an exact differential because #(del/(delV)((delP)/(delT))_V)=(del/(delT)((delP)/(delV))_T)#
That is very easily calculable, however I'm not sure how to set up the equation to prove that đq is an inexact differential.
I understand that heat is a path function and this:
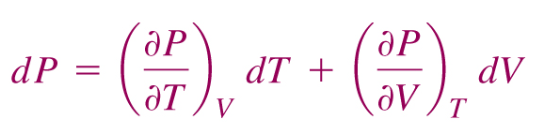
Where dP is an exact differential because
That is very easily calculable, however I'm not sure how to set up the equation to prove that đq is an inexact differential.
1 Answer
An exact differential would have that the cross-derivatives are equal.
For example, we know that
#dG = -SdT + VdP = ((delG)/(delT))_PdT + ((delG)/(delP))_TdP#
so we would have that
#(del)/(delP)[((delG)/(delT))_P]_T = (del)/(delT)[((delG)/(delP))_T]_P#
or
#-((delS)/(delP))_T = ((delV)/(delT))_P# .
For the first law of thermodynamics, we have:
#dU = deltaq + deltaw# where
#delta# indicates an inexact differential and#d# indicates an exact differential.
A reversible process with PV-only work in general would have that:
#dU = deltaq_(rev) - PdV#
By definition, the constant-volume heat capacity is
#C_V = ((delU)/(delT))_V# ,
so
#C_VdT + PdV = deltaq_(rev)#
If we took the cross-derivatives at this point:
#((del C_V)/(delV))_T stackrel(?" ")(=) ((delP)/(delT))_V#
The constant-volume heat capacity is only a function of temperature for ideal gases, so:
#0 ne ((delP)/(delT))_V#
So, at this point,
#C_V/TdT + P/TdV = (deltaq_(rev))/T#
We recognize this as the entropy,
Right now,
#((del(C_V//T))/(delV))_T stackrel(?" ")(=) ((del(nR//V))/(delT))_V#
This now does yield

